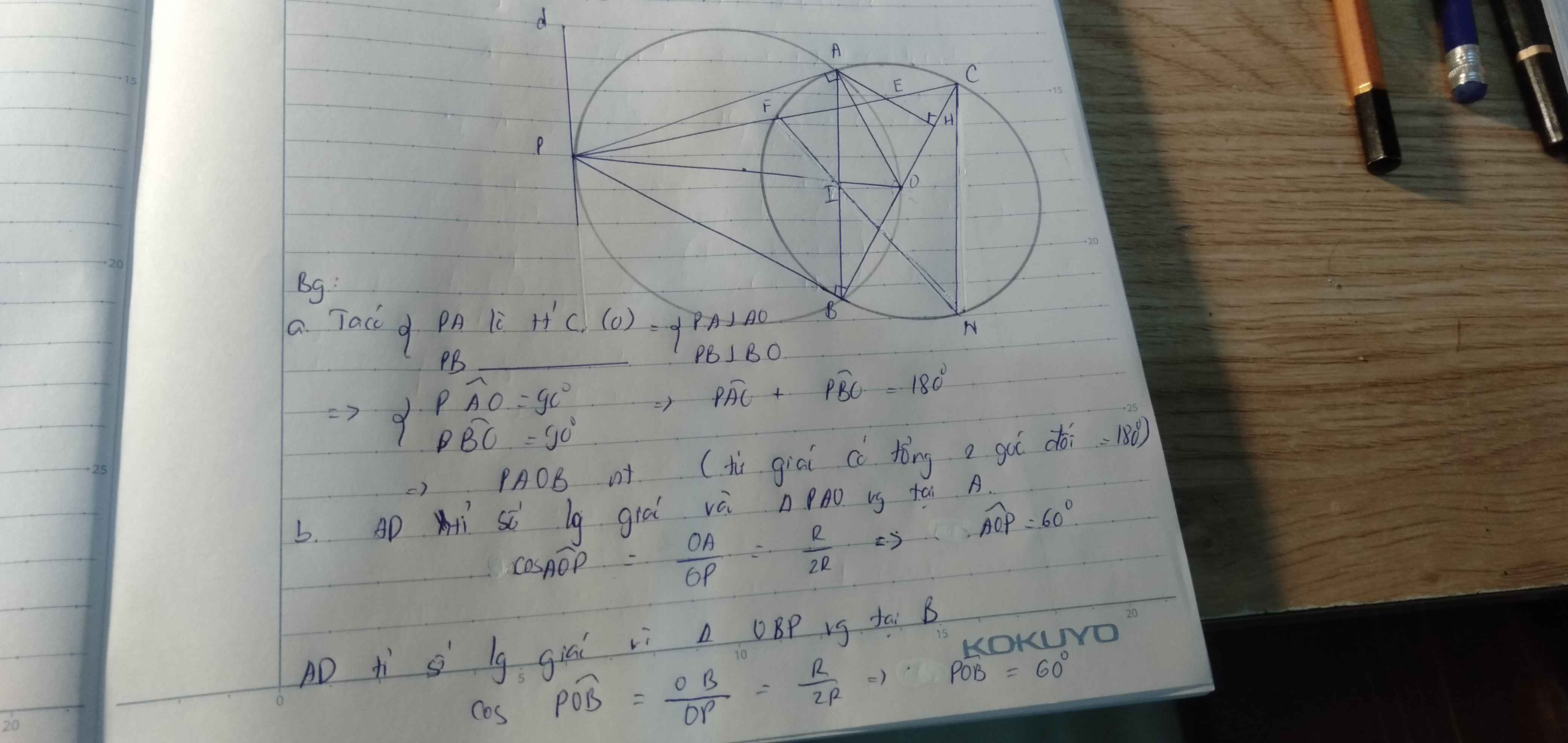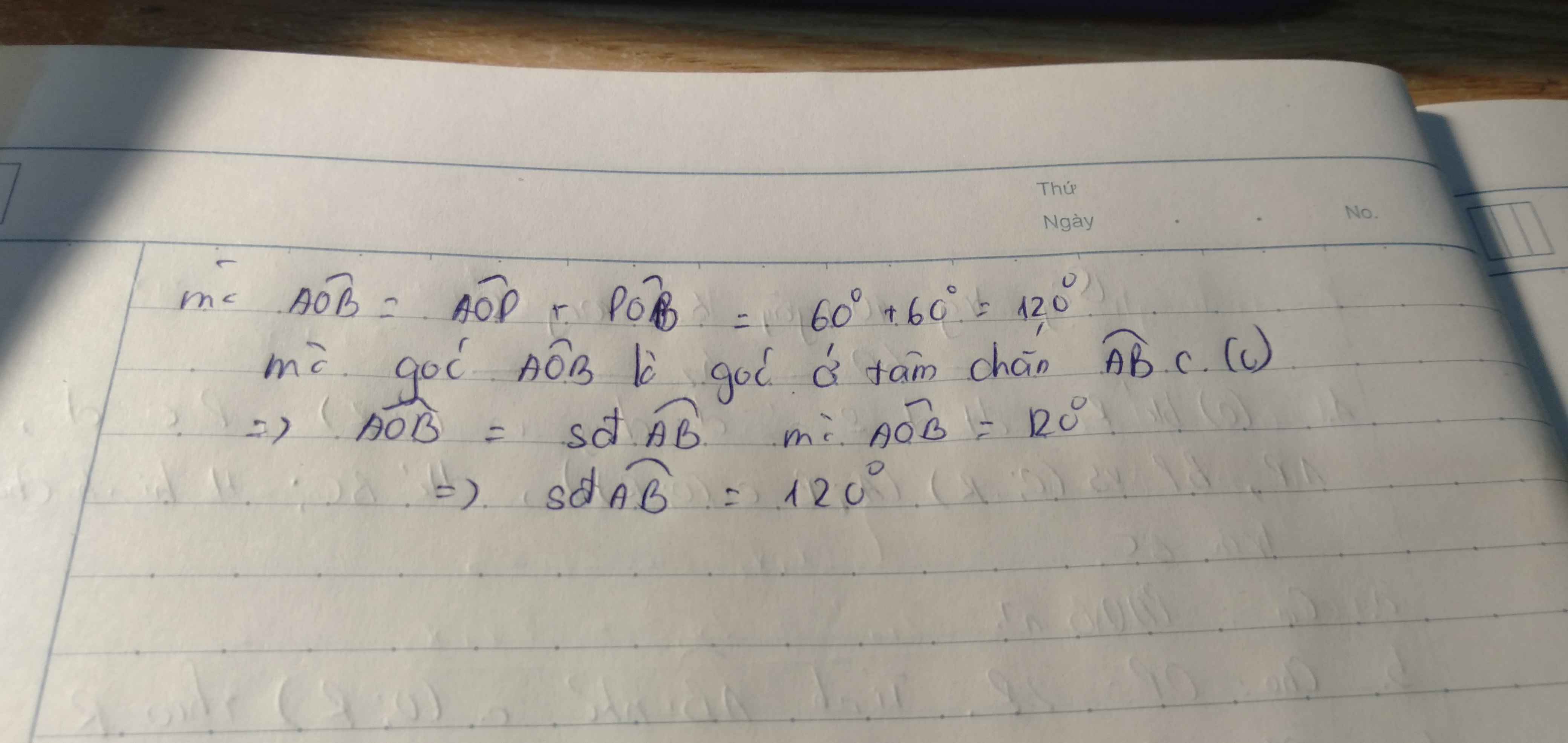cho đường tròn (O,R) và đường thẳng d không có điểm chung sao cho khoảng cách từ O đến d không quá 2R .Qua điểm M trên d ,vẽ các tiếp tuyến MA,MB tớ (O) với A,B là các tiếp điểm .gọi h là hình chiếu vuông góc của O trên d .dây OB cắt OH ở K và cắt OM tại I .tia OM cắt (O) tại K
A) chứng minh năm điểm O,A,M,B,H thuộc cùng một đường tròn
b)chứng minh OM ⊥AB và OI.OM =R2
c)chứng minh OK.OH =OI.OM
d)tìm vị trí của điểm M trên D để tứ giác OAEB là hình thoi