Người ta giữ cho một thanh AB hình trụ ( có khối lượng m=50kg) nghiêng một góc α so với mặt sàn nằm ngang bằng cách tác dụng vào đầ A một lực F vuông góc với trục AB của khúc gỗ và nằm trong mặt phẳng thẳng đứng . Lấy g=10m/s2 . Tìm độ lớn của F, Hướng cà đọ lớn của phản lực tác dụng lên đầu của khúc gỗ trong các trường hợp:
a) α= 30o
b) α=...
Đọc tiếp
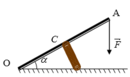
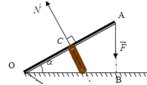
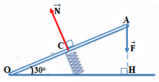
Người ta giữ cho một thanh AB hình trụ ( có khối lượng m=50kg) nghiêng một góc α so với mặt sàn nằm ngang bằng cách tác dụng vào đầ A một lực F vuông góc với trục AB của khúc gỗ và nằm trong mặt phẳng thẳng đứng . Lấy g=10m/s2 . Tìm độ lớn của F, Hướng cà đọ lớn của phản lực tác dụng lên đầu của khúc gỗ trong các trường hợp:
a) α= 30o
b) α= 60o
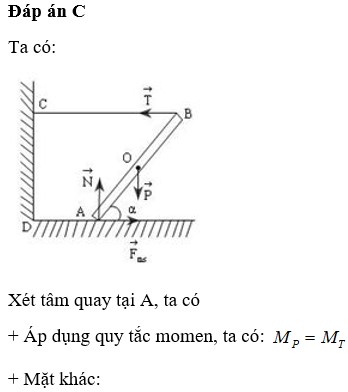
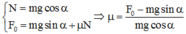
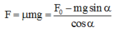
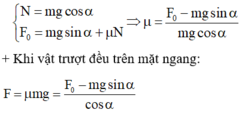
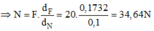
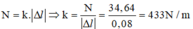
Ta có :
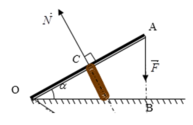
Trọng lực của thanh đặt ở trung điểm thanh (gọi G là trung điểm thanh AB)
Ta giải bài toán trong trường hợp tổng,
Áp dụng quy tắc momen trục quay tại B:
\(mg.BGsin\alpha=F.BA\)
\(\rightarrow F=mg\frac{BGsin\alpha}{BA}=50.10\frac{sin\alpha}{2}=250sin\alpha\)
Phản lực của tường phải cân bằng với F và P.
Phản lực theo phương ngang: \(N_x=F.sin\alpha\)
Phản lực theo phương thẳng đứng:\(N_y=mg-F.cos\alpha\)
Gọi góc hợp giữa phản lực và phương ngang là \(\phi\)
\(tan\phi=\frac{Ny}{Nx}=\frac{mg-Fcos\alpha}{Fsin\alpha}\)
\(=\frac{500-250sin\alpha.cosalpha}{250sinalpha^2}=\frac{2-sin\alpha.cosalpha}{sinalpha^2}\)
Độ lớn của phản lực:
\(N=\sqrt{N_x^2+N^2_y}=\sqrt{F^2+m^2g^2-2mgFcosalpha}\)
Trong 2 trường hợp góc α này chúng ta thay số và tìm các giá trị cần tìm