Cho tam giác ABC vuông tại A có góc C bằng \(60^o\). Vẽ tia phân giác của góc C cắt cạnh AB tại D .Trên cạnh CB lấy điểm M sao cho CM = CA a ) Chứng minh \(\Delta ACD=\Delta MCD\) b ) Qua C vẽ đườn...

TQ

Trần Quốc Tuấn hi

10 tháng 12 2019

Cho tam giác ABC vuông tại A có góc C bằng \(60^o\). Vẽ tia phân giác của góc C cắt cạnh AB tại D .Trên cạnh CB lấy điểm M sao cho CM = CA a ) Chứng minh \(\Delta ACD=\Delta MCD\) b ) Qua C vẽ đường thẳng xy vuông góc với CA cắt tia DM ở N . Chứng minh BN và CD song song với nhau Các bạn giúp mình nhé : Bạn Vũ Minh Tuấn , Nguyễn Việt Lâm , Nguyễn Văn Đạt , Băng Băng 2k6 và thầy Akai Haruma , Phynit và cùng với tất cả các...

Đọc tiếp

#Toán lớp 7

1

VM

Vũ Minh Tuấn

10 tháng 12 2019

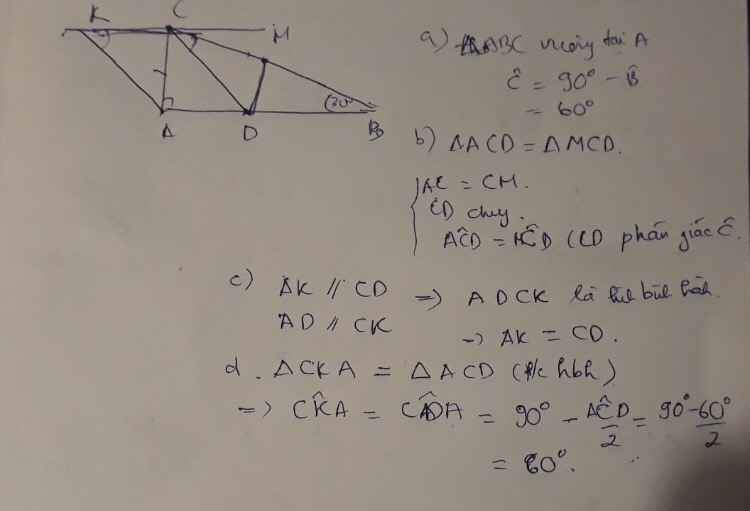
Hình bạn tự vẽ nha!

a) Xét 2 \(\Delta\) \(ACD\) và \(MCD\) có:

\(AC=MC\left(gt\right)\)

\(\widehat{ACD}=\widehat{MCD}\) (vì \(CD\) là tia phân giác của \(\widehat{C}\))

Cạnh CD chung

=> \(\Delta ACD=\Delta MCD\left(c-g-c\right).\)

b) Mình nghĩ đã nhé.

Chúc bạn học tốt!

Đúng(0)

NH

Nguyen Hoang

13 tháng 12 2021

Cho ∆ABC vuông tại A có góc B = 300.a) Tính sốđo góc C.b) Vẽ tia phân giác của góc C cắt cạnh AB tại D. Trên cạnh CB lấy điểm M sao cho CM = CA. Chứng minh ∆ACD = ∆MCD. c) Qua C vẽ đường thẳng xy vuông góc CA. TừA kẻđường thẳng song song với CD cắt xy ởK.Chứng minh AK = CD. d) Tính góc...

Đọc tiếp

#Toán lớp 7

0

EK

Earth-K-391

29 tháng 12 2021

cho tam giác ABC vuông tại A có góc B=30⁰

a) tính góc C

b) vẽ tia phân giác của góc cắt cạnh AB tại D

c) Trên cạnh CB lấy điểm M sao cho CM=CA. CM tam giác ACD = tam giác MCD

d) Qua C vẽ đường thẳng xy vuông góc với CA. Từ A kẻ đường thẳng song song với CD cắt xy ở K. CM: AK=CD

e) tính góc AKC

#Toán lớp 7

1

NH

Nguyễn Hoàng Minh

29 tháng 12 2021

undefined

Đúng(2)

KP

Không Phải Dạng Vừa Đâu

11 tháng 7 2017 - olm

Cho tam giác ABC vuông tại A có góc B = 30 độ .

a) Tính góc C

b) vẽ tia phân giác của góc C cắt cạnh AB tại D . Trên cạnh CB lấy điểm M sao cho CM = CA . CMR : tam giác ACD = tam giác MCD .

Qua C vẽ đường thẳng xy vuông góc CA . Từ A kẻ đường thẳng // vs CD cắt xy ở K . Cm : AK = CD

c) tính góc AKC

#Toán lớp 7

2

LT

lê thị thu huyền

11 tháng 7 2017

mình vẽ hình rồi, còn phần chứng minh làm như bạn Trần Hoàng Việt nha!!

Đúng(2)

A

๖ACE✪Hoàngミ★Việtツ

11 tháng 7 2017

a) Ta có : A=90⁰ ; B=30⁰

=> C=180-A-B=180-90-30=60

b) Xét tam giác ACD và MCD ta có :

CD chung (1)

CM=CA (gt)(2)

góc ACD=góc DCM (gt) (3)

Từ (1)(2)(3) =>\(\Delta\)ACD=\(\Delta\)MCD (c.g.c)

c) Ta có :AK//CD; CK//AD => tứ giác ADCK là hình bình hành

=>AK=CD (cặp cạnh tương ứng )

d)Ta có : \(\widehat{BDC}\)=180-30-60:2=120⁰

\(\widehat{CPA}\)=180-120=60

Do ADCK là hình bình hành nên \(\widehat{CPA}\)=\(\widehat{AKC}\)=\(60^0\)

Đúng(1)

HL

Hai Long

11 tháng 12 2021

Cho ∆ABC vuông tại A có góc B = 300 . a) Tính số đo góc C.

b) Vẽ tia phân giác của góc C cắt cạnh AB tại D. Trên cạnh CB lấy điểm M sao cho CM = CA. Chứng minh ∆ACD = ∆MCD.

c) Qua C vẽ đường thẳng xy vuông góc CA.

Từ A kẻ đường thẳng song song với CD cắt xy ở K.

Chứng minh AK = CD. d) Tính góc AKC.

#Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

11 tháng 12 2021

a: \(\widehat{C}=60^0\)

Đúng(1)

QC

Quỳnh Chi

29 tháng 6 2021 - olm

Cho tam giác ABC vuông tại A có góc ABC bằng 35độ a, Tính số đo góc ACB b,Vẽ tia phân rác của góc ACB cách cạnh AB tại D.Trên cạnh CB lấy điểm M sao cho CM = CA . Chứng minh ACD = MCD c, Qua C vẽ đường thẳng xy vuông góc với CA.Từ A kẻ đường thẳng song song với CD cắt xy ở K . Chứng minh AK=CD d, qua B vẽ đường thẳng vuông góc với CD tại H và cắt tia CA tại N. Chứng minh 3 điểm M,D,N thẳng hàng...

Đọc tiếp

#Toán lớp 7

2

QC

Quỳnh Chi

29 tháng 6 2021

Các bạn giúp mik nha!!!

Đúng(0)

CH

chu hải minh

29 tháng 6 2021

mik chịu thui hihi

Đúng(0)

Y

Yubi

8 tháng 7 2015 - olm

Cho \(\Delta\)ABC vuông tại A có góc B= \(30^o\)a) Tính góc Cb) Vẽ tia phân giác của góc C cắt cạnh Ab tại D. Trên cạnh CB lấy điểm M sao cho CM=CA. Chứng minh: \(\Delta\)ACD=\(\Delta\)MCD. Qua C vẽ đường thẳng xy vuông góc CA. Từ A kẻ đường thẳng song song với CD cắt xy ở K. Chứng minh: AK= CDc) Tính góc...

Đọc tiếp

#Toán lớp 7

3

TT

Trần Tuyết Như

8 tháng 7 2015

mk viết ngắn gọn thui nhé:

a) góc C = 180⁰ - Â - B = 180⁰- 90⁰ - 30⁰ = 60⁰

b) * tam giác ACD = tam giác MCD (c.g.c) . Vì:

CD : cạnh chung

góc ACD = góc MCD

AC = MC

* Xét 2 tam giác vuông: ACK và CDA:

góc ACD = góc CAK (2 góc so le trong)

AC : cạnh chung

=> tam giác ACK = tam giác CDA (cạnh góc vuông - góc nhọn kề)

=> AK = CD (2 cạnh tương ứng)

c) theo câu b: tam giác ACK = tam giác CDA (cạnh góc vuông - góc nhọn kề)

=> góc AKC = góc ADC (2 góc tương ứng)

Trong tam giác ACD, có:

góc ADC = 180⁰ - góc A - (góc ACB : 2) = 180⁰ - 90⁰ - 60⁰: 2 = 60⁰

=> góc AKC = góc ADC = 60⁰

Đúng(0)

DT

Dương Tũn

8 tháng 7 2015

Đúng(0)

NH

Nguyễn Hoàng Đức

22 tháng 8 2019 - olm

Nếu được vẽ hộ mình với

Cho tam giác ABC vuông tại A có B = 30 độ

a) Tính góc C

b) Vẽ tia phân giác của góc C, cách cạnh AB tại D. Trên cạnh CB lấy điểm M sao cho CM=CA. Chứng minh: tam giác ACB = tam giác MCD

c) Qua C vẽ đường thẳng XY vuông góc CA. Từ A kẻ đường thẳng sonh song với CD cắt XY ở K. Chứng minh AK=CD

d) tính góc AKC

#Toán lớp 7

5

NH

Nhật Hạ

22 tháng 8 2019

a, Xét ∆ABC vuông tại A có: B + C = 90^o

=> 30^o + C = 90^o

=> C = 60^o

b, Vì CD là tia phân giác của C

=> ACD = DCB = ACB/2 = 60^o/2 = 30^o

Xét ∆ACB và ∆MCD

Có: AD: cạnh chung (gt)

ACD = DCM (vì CD là tia p/g của C)

CA = CM (gt)

=> ∆ACB = ∆MCD (c.g.c)

c, XY vuông góc CA => KCA = 90^o

Vì AK // CD => CKA = CDA (2 góc so le trong)

Xét ∆CAK vuông tại C và ∆ADC vuông tại A

Có: CA: cạnh chung

CKA = CDA (cmt)

=> ∆CAK = ∆ADC (cgv-gn)

=> AK = DC (2 cạnh tương ứng)

d, Vì ∆CAK = ∆ADC (câu c)

=> KAC = ACD (2 góc tương ứng)

Mà ACD = 30^o

=> KAC = 30^o

Xét ∆KAC vuông tại C có: KAC + AKC = 90^o

=> 30^o + AKC = 90^o

=> AKC = 60^o

Đúng(0)

K

Kan

22 tháng 8 2019

quên vẽ hình :( đường thẳng xy tự điền chữ vào cái đường thẳng trên cùng nhé :(( srr vì quên

Đúng(0)

T

tranviehien

24 tháng 11 2016 - olm

Cho tam giác ABC vuông tại A có góc B = 30 độ
a) tính góc C
b)vẽ tia phân giác của góc C cắt cạnh AB tại D
c) trên cạnh CB lấy điểm M sao cho CM=CẢ.chứng minh tam giác ACD= tam giac MCD
d)qua C vẽ đường thẳng xy vuông góc CA.từ A kẻ đường thẳng song song với CD cắt xyK. chứng minh AK=CD
ế) tính góc AKC
(giúp em với mai em phải nộp r)

#Toán lớp 7

1

HM

hatsume miku

24 tháng 3 2019

a. Ta có A+B+C=180 độ ( tổng 3 góc trong tam giác)

=> C= 180 độ - ( A+B) =60 độ

b. Xét 2 tam giác vuông : tam giác : DCA và DCM có :

DC chung; góc DCA = góc DCM ( cd là phân giác của acm ); CM=CA (gt)

=>tam giác DCM=tam giác DCA (c.g.c)

c. xét hai tam giác vuông : DCA và KAC có :

AC chung; góc DCA = góc CAK ( so le trong vì DC // AK )

=> DCA=KAC(cgv. gn )=>AK=CD(2 góc tương ứng )

d. ta có: tam giác : DCA = KAC ( câu c)=>AKC=ADC (2 góc tương ứng)

Mà CAK+AKC+KCA=180 độ ( tổng 3 góc trong tam giác)

=>AKC= 180-90-30=60 độ

vì KAC=ACD60/2=30 độ

Đúng(0)

PT

Phạm Thùy Dung

10 tháng 12 2019 - olm

Cho tam giác ABC vuông tại A có góc C bằng 60o60o. Vẽ tia phân giác của góc C cắt cạnh AB tại D .Trên cạnh CB lấy điểm M sao cho CM = CA

a ) Chứng minh ΔACD=ΔMCD

b ) Qua C vẽ đường thẳng xy vuông góc với CA cắt tia DM ở N . Chứng minh BN và CD song song với nhau

#Toán lớp 7

0

6N

6.Vũ Nguyễn Hiếu lớp 7/8

25 tháng 11 2021

Cho \(\Delta ABC\) vuông tại A (AB>AC).Vẽ tia phân giác của góc C cắt AB tại D.Trên cạnh BC lấy điểm E sao cho CE=CA a)Chứng minh:\(\Delta CDA=\Delta CDE\) và \(DE\perp BC\)b)Qua C vẽ đường thẳng vuông góc với AC.Qua A vẽ đường thẳng song song với CD,hai đường này cắt nhau tại M.Chứng minh: AM=CDc)Qua B vẽ đường thẳng vuông góc với CD tại N và cắt AC tại K.Chứng minh:AK=BEvà K;E;D thẳng hàng. (❤Mọi...

Đọc tiếp

#Toán lớp 7

0

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP