Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau trên \([\)0;3\(]\):
X4-8x3+20x2-16x-16x+8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 1:
$y=-2x^2+4x+3=5-2(x^2-2x+1)=5-2(x-1)^2$
Vì $(x-1)^2\geq 0$ với mọi $x\in\mathbb{R}$ nên $y=5-2(x-1)^2\leq 5$
Vậy $y_{\max}=5$ khi $x=1$
Hàm số không có min.
Câu 2:
Hàm số $y$ có $a=-3<0; b=2, c=1$ nên đths có trục đối xứng $x=\frac{-b}{2a}=\frac{1}{3}$
Lập BTT ta thấy hàm số đồng biến trên $(-\infty; \frac{1}{3})$ và nghịch biến trên $(\frac{1}{3}; +\infty)$
Với $x\in (1;3)$ thì hàm luôn nghịch biến
$\Rightarrow f(3)< y< f(1)$ với mọi $x\in (1;3)$
$\Rightarrow$ hàm không có min, max.

f(x) = 2sinx + sin2x trên đoạn [0; 3 π /2]
f′(x) = 2cosx + 2cos2x = 4cos(x/2).cos3(x/2)
f′(x) = 0
⇔ 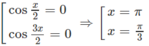
Ta có: f(0) = 0,
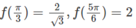
Từ đó ta có: min f(x) = −2 ; max f(x) = 3 3 /2

Đáp án B
Cách 1: Tư duy tự luận
Xét hàm số f x = sin x 1 + cos x trên 0 ; π
Đạo hàm f ' x = cos x 1 + cos x − sin 2 x = 2 cos 2 x + cos x − 1 ;
f ' x ⇔ cos x = − 1 cos x = 1 2 ⇔ x = π + k 2 π x = ± π 3 + k 2 π k ∈ ℤ
Do x ∈ 0 ; π nên x = π 3 ; x = π .
Ta có
f 0 = f π = 0 ; f π 6 = 3 3 4
Vậy
M = max 0 ; π f x = 3 3 4 ; m = min 0 ; π f x = 0
Cách 2: Sử dụng máy tính cầm tay
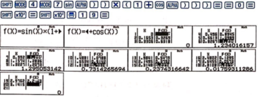
Quan sát bảng giá trị, ta thấy
M = max 0 ; π f x ≈ 1,295... ≈ 3 3 4 ; m = min 0 ; π f x = 0

\(f\left(x\right)=e^{sinx}-sinx-1\)
\(\Rightarrow f'\left(x\right)=cosx.e^{sinx}-cosx=cosx\left(e^{sinx}-1\right)\)
\(f'\left(x\right)=0\Leftrightarrow\left[{}\begin{matrix}cosx=0\\sinx=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{\pi}{2}\\x=\pi\end{matrix}\right.\)
\(f\left(0\right)=0\) ; \(f\left(\dfrac{\pi}{2}\right)=e-2\) ; \(f\left(\pi\right)=0\)
\(\Rightarrow f\left(x\right)_{min}=0\) ; \(f\left(x\right)_{max}=e-2\)

TXĐ: D = R\{0}
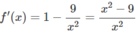
f′(x) = 0 ⇔ x = 3 hoặc x = -3
Hàm số nghịch biến trong các khoảng (-3;0), (0;3) và đồng biến trong các khoảng (− ∞ ;3), (3;+ ∞ )
Bảng biến thiên:
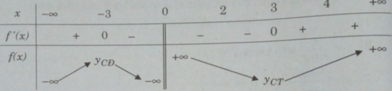
Ta có: [2;4] ⊂ (0; + ∞ ); f(2) = 6,5; f(3) = 6; f(4) = 6,25
Suy ra
min f(x) = f(3) = 6; max f(x) = f(2) = 6,5
TXĐ: D = R\{0}
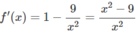
f′(x) = 0 ⇔ x = 3 hoặc x = -3
Hàm số nghịch biến trong các khoảng (-3;0), (0;3) và đồng biến trong các khoảng (− ∞ ;3), (3;+ ∞ )
Bảng biến thiên:

Ta có: [2;4] ⊂ (0; + ∞ ); f(2) = 6,5; f(3) = 6; f(4) = 6,25
Suy ra
min f(x) = f(3) = 6; max f(x) = f(2) = 6,5

a) 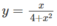 trên khoảng (−
∞
;+
∞
);
trên khoảng (−
∞
;+
∞
);
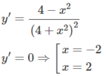
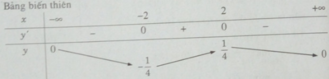
Từ đó ta có min f(x) = −1/4; max f(x) = 1/4
b) 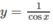 trên khoảng
trên khoảng 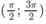
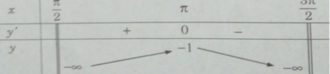
y′ = 0 ⇔ x = π
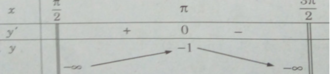
Hàm số không có giá trị nhỏ nhất. Giá trị lớn nhất của hàm số là: max y = y(π) = −1.

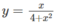 trên khoảng (−
∞
;+
∞
);
trên khoảng (−
∞
;+
∞
);
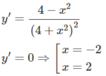
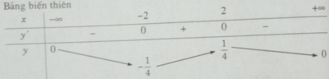
Từ đó ta có min f(x) = −1/4; max f(x) = 1/4

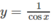 trên khoảng
trên khoảng 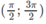
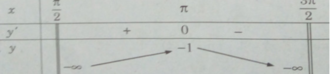
y′ = 0 ⇔ x = π
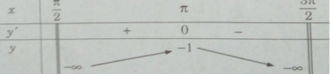
Hàm số không có giá trị nhỏ nhất. Giá trị lớn nhất của hàm số là: max y = y( π ) = −1