1/ Cho nửa đường tròn (O) đường kính AB, kẻ các tiếp tuyến Ax và By( Ax, By và nửa mặt phẳng bờ AB có chứa đường tròn thuộc cùng 1 phía). M là một điểm nằm trên cung AB, kẻ tiếp tuyến M cắt Ax tại C và By tại D. Đoạn thẳng AD và BC cắt nhau tai N. CMR MN//BD
2/ Cho hình vuông ABCD. Kẻ từ A cắt BC tại E và cắt CD tại F. CMR 1/AB^2=1/AE^2+1/AF^2
3/
a/ Cho x,y ∈ N, tìm nghiệm nguyên của 2xy^2 + x + y + 1 = x^ + 2y^2 + xy
b/ Cho x,y ∈ N và x+y+z = 1
Tìm giá trị nhỏ nhất của A = 1/16x + 1/4y + 1/z
Giải hộ mình với!!! Mình mới đi thi ở trường, có vài câu quên cách làm với không biết làm, mong mọi người chỉ mình.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
CM là tiếp tuyến có M là tiếp điểm
CA là tiếp tuyến có A là tiếp điểm
Do đó: CM=CA
Xét (O) có
DM là tiếp tuyến có M là tiếp điểm
DB là tiếp tuyến có B là tiếp điểm
Do đó: DM=DB
Ta có: CM+MD=CD
mà CM=CA
và DM=DB
nên CD=CA+DB

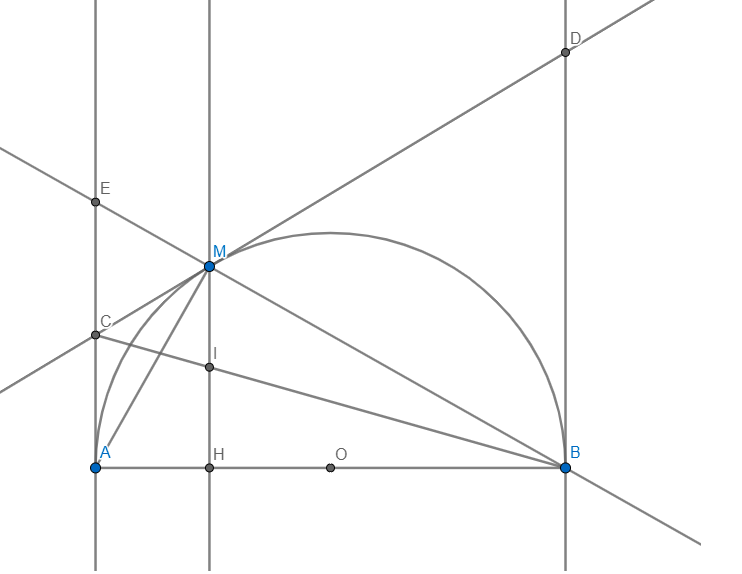
c) BM cắt Ax tại E.BC cắt MH tại I
Vì AB là đường kính nên \(\angle AMB=90\)
Vì CM,CA là tiếp tuyến nên \(CM=CA\)
Ta có tam giác AME vuông tại M có \(CM=CA\Rightarrow C\) là trung điểm AE
Vì \(MH\parallel AE(\bot AB)\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{IH}{AC}=\dfrac{BI}{BC}\\\dfrac{IM}{CE}=\dfrac{BI}{BC}\end{matrix}\right.\Rightarrow\dfrac{IH}{AC}=\dfrac{IM}{CE}\)
mà \(AC=CE\Rightarrow IH=IM\) nên ta có đpcm

a: Xét tứ giác CAOM có góc CAO+góc CMO=180 độ
nên CAOM là tứ giác nội tiếp
Tâm là trung điểm của OC
b: Xét (O) có
CM,CA là các tiếp tuyến
nên CM=CA và OC là phân giác của góc MOA(1)
Xét (O) có
DM,DB là các tiếp tuyến
nên DM=DB và OD là phân giác của góc MOB(2)
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
AC+BD=CM+MD=CD

Xét (O) có
CM,CA là các tiếp tuyến
nên CM=CA và OC là phân giác của góc MOA(1)
mà OM=OA
nên OC là đường trung trực của MA
=>OC vuông góc với MA tại I
Xét (O) có
DM,DB là các tiếp tuyến
nên DM=DB và OD là phân giác của góc MOB(2)
mà OM=OB
nên OD là trung trực của BM
=>OD vuông góc với BM
Từ (1) và (2) suy ra góc COD=1/2*180=90 độ

a: Xét tứ giác OBDM có
góc OBD+góc OMD=180 độ
=>OBDM là tư giác nội tiếp
c: Xét ΔKOB và ΔKFE có
góc KOB=góc KFE
góc OKB=góc FKE
=>ΔKOB đồng dạng với ΔKFE
=>KO/KF=KB/KE
=>KO*KE=KB*KF

1: Xét (O) có
CA là tiếp tuyến có A là tiếp điểm
CM là tiếp tuyến có M là tiếp điểm
Do đó: OC là tia phân giác của \(\widehat{MOA}\)
Xét (O) có
DB là tiếp tuyến có B là tiếp điểm
DM là tiếp tuyến có M là tiếp điểm
Do đó: OD là tia phân giác của \(\widehat{MOB}\)
Ta có: \(\widehat{COD}=\widehat{COM}+\widehat{DOM}\)
\(=\left(\widehat{MOA}+\widehat{MOB}\right)\cdot\dfrac{1}{2}\)
\(=180^0\cdot\dfrac{1}{2}=90^0\)
hay ΔCOD vuông tại O
Xét (O) có
CA là tiếp tuyến có A là tiếp điểm
CM là tiếp tuyến có M là tiếp điểm
Do đó: CM=CA
Xét (O) có
DB là tiếp tuyến có B là tiếp điểm
DM là tiếp tuyến có M là tiếp điểm
Do đó: DB=DM
\(AC\cdot BD=CM\cdot MD=OM^2\) không phụ thuộc vào vị trí của M

Bạn có thể tham khảo bài tương tự ở đây:
BT: Cho nửa đường tròn (O;R) đường kính AB. Kẻ 2 tiếm tuyến Ax, By của nửa đường tròn (O). Qua M thuộc nửa đường tròn (... - Hoc24
CM góc COD = 90 độ
Theo tính chất 2 tiếp tuyến cắt nhau
Ta có : OC là phân giác góc AOM
=> góc COM = 1/2 góc AOM
OD là phân giác góc BOM
=> góc DOM = 1/2 góc BOM
=> góc COD = góc COM + góc DOM = 1/2 ( góc AOM + góc BOM ) = 1/2 góc AOB = 1/2 x 180 độ = 90 độ
