Dựng tam giác ABC biết góc A = 60 độ, các đường cao BD=2,5cm, CE=3cm.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 2 2022
Xét ΔABD vuông tại D và ΔACE vuông tại E có
\(\widehat{A}\) chung
Do đó: ΔABD\(\sim\)ΔACE
Suy ra: AB/AC=AD/AE
hay AB/AD=AC/AE
Xét ΔABC và ΔADE có
AB/AD=AC/AE
\(\widehat{A}\) chung
Do đó: ΔABC\(\sim\)ΔADE
Suy ra: \(\widehat{ABC}=\widehat{ADE}=60^0;\widehat{ACB}=\widehat{AED}=50^0\)
=>\(\widehat{EDC}=120^0;\widehat{DEB}=130^0\)
QN
1
7 tháng 8 2023
Xét tứ giác BEDC có
góc BEC=góc BDC=90 độ
=>BEDC là tứ giác nội tiếp
=>góc AED=góc ACB
Xét ΔAED và ΔACB có
góc AED=góc ACB
góc A chung
=>ΔAED đồng dạng với ΔACB
=>S AED/S ACB=(AE/AC)^2=(cos60)^2=1/4
=>S AED=1/4*S ACB
PT
1
CM
1 tháng 4 2019
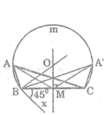
- Dựng đoạn thẳng AB = 3cm
- vẽ tia Bx sao cho góc (CBx) = 45 °
- Dựng trung điểm M của BC
- Dựng đường trung trực của BC (qua M)
- Dựng tia vuông góc với Bx tại B ,cắt đường trung trực của BC tại O
- Dựng cung tròn BmC bán kính OB là cung chứa góc 45 ° vẽ trên đoạn BC
- Dựng đường tròn tâm M bán kính 2,5cm cắt cung BmC lần lượt tại A và A’
- Nối AB , AC (hoặc A’B , A’C) ta có: ∆ ABC ( ∆ A’BC) có BC = 3cm , góc A = 45 ° (hoặc góc (A' ) =45°) và trung tuyến AM =2,5cm
30 tháng 1 2022
Xét ΔDBC vuông tại D và ΔECB vuông tại E có
BC chung
\(\widehat{DCB}=\widehat{EBC}\)
Do đó: ΔDBC=ΔECB
Suy ra: \(\widehat{IBC}=\widehat{ICB}\)
=>ΔICB cân tại I
=>\(\widehat{DBC}=\dfrac{180^0-110^0}{2}=35^0\)
\(\Leftrightarrow\widehat{ACB}=90^0-35^0=55^0\)
\(\Leftrightarrow\widehat{ABC}=55^0\)
hay \(\widehat{BAC}=70^0\)
HP
1
13 tháng 5 2019
\(\Delta ACE\)vuông tại A có \(\widehat{A}=60^o\)nên \(\widehat{ACE}=30^o\)
\(\Rightarrow\frac{AE}{AC}=\frac{1}{2}\)
Tương tự : \(\frac{AD}{AB}=\frac{1}{2}\)
\(\Rightarrow\frac{AE}{AC}=\frac{AD}{AB}\Rightarrow\frac{AE}{AD}=\frac{AC}{AB}\)
chứng minh : \(\Delta ADE\approx\Delta ABC\)( c.g.c )
\(\Rightarrow\frac{S_{ADE}}{S_{ABC}}=\left(\frac{AD}{AB}\right)^2=\frac{1}{4}\)
\(\Rightarrow S_{ADE}=\frac{1}{4}S_{ABC}\)
NK
0