Cho tam giác ABCABC có ˆB=ˆCB^=C^. Tia phân giác góc AA cắt BCBC tại D.D. Chứng minh...
Đọc tiếp
Cho tam giác có . Tia phân giác góc cắt tại Chứng minh rằng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
29 tháng 6 2018
Giải:
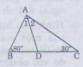
Theo định lí tổng ba góc trong một tam giác ta có:
ˆBAC+ˆB+ˆC=1800BAC^+B^+C^=1800
ˆBAC=1800−(ˆB+ˆC)BAC^=1800−(B^+C^) = 1800−(800+300)=7001800−(800+300)=700
Vì ADAD là tia phân giác của ˆBACBAC^ nên ˆA1A1^=ˆA2A2^
ˆA1A1^=ˆA2A2^=ˆA2A^2=7002=3507002=350
ˆADCADC^ = ˆBB^ + ˆA1A1^(Góc ngoài của tam giác)
=800+350=1150=800+350=1150
Hai góc ˆADCADC^ và ˆADBADB^ là hai góc kề bù
Do đó ˆADBADB^= 1800−ˆADC1800−ADC^= 1800−1150=650
11 tháng 8 2021
Sửa đề: góc b=góc c
Xét ΔABC có \(\widehat{B}=\widehat{C}\)
nên ΔABC cân tại A
Suy ra: AB=AC
Ta có: ΔABC cân tại A
mà AD là đường phân giác ứng với cạnh BC
nên D là trung điểm của BC
hay DB=DC
1 tháng 12 2017
Tam giác ABC có góc B = góc C
=> ABC là tam giác cân (hai góc kề cạnh đáy bằng nhau)
=> AB = AC
Xét hai tam giác BAD và CAD có:
AC = AB (cmt)
góc BAD = góc CAD (AD là phân giác của góc A)
góc B = góc C (gt)
=> tam giác BAD = tam giác CAD (g.c.g)
=> DB = DC
PT
1
21 tháng 3 2023
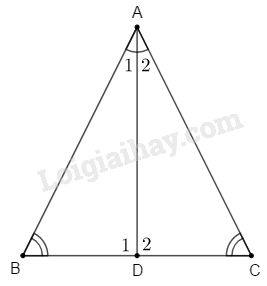
a: Xét ΔABD và ΔACD có
AB=AC
góc BAD=goc CAD
AD chung
=>ΔABD=ΔACD
b: ΔABD=ΔACD
=>BD=CD
c: ΔACB cân tại A
mà ADlà trung tuyến
nên AD vuông góc BC
LA
0
KT
0
ST
0