Cho hbh ABCD, BC=2AD. Góc BAD = 60 độ. E,F làn lượt là trung điểm AD,BC. Tính góc AED?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 2 2022
a: Xét tứ giác ABED có
BE//AD
Do đó:ABED là hình thang
b: Xét tứ giác ABEF có
AF//BE
AF=BE
Do đó: ABEF là hình bình hành
mà AB=AF
nên ABEF là hình thoi
SUy ra: EF=AF=AD/2
Xét ΔEAD có
EF là đường trung tuyến
EF=AD/2
Do đó: ΔEAD vuông tại E
hay \(\widehat{AED}=90^0\)
19 tháng 11 2016
a ,
Ta có BE//AD => ABED là hình thang
xét tam giác CED có EC=DC và có góc C=60°
=>CED là tam giác đều
=>EDC=60°
ta có BDE=D-ECD (đây là ký hiệu góc)
=>BDE=60°
Mà ta biết góc A=60°
Hình thang ABED có 2 góc đáy bằng nhau => là hình thang cân
b ,
Ta có :
CE = BE
DF=FA
->EF là đường trung bình của hình bình hành ABCD .
-> AB // EF // CD mà EB // AF ( E , F thuộc AD và BC )
-> Tứ giác ABEF là hình bình hành .
-> EF = AB mà AD = BC = 2AB
-> AD = 2EF
Xét tam giác AED có : đường trung tuyến EF ứng với cạnh huyền AD và
EF = 1/2 AD nên tam giác AED là tam giác vuông tại E
-> Góc AED = 90 độ .
20 tháng 10 2023
Sửa đề: BC=2AB
a: \(BE=EC=\dfrac{BC}{2}\)
\(AF=FD=\dfrac{AD}{2}\)
mà BC=AD
nên BE=EC=AF=FD
Xét tứ giác ABEF có
BE//AF
BE=AF
Do đó: ABEF là hình bình hành
mà BE=BA(=1/2BC)
nên ABEF là hình thoi
b: Xét ΔIFA có
FB là đường trung tuyến
\(FB=\dfrac{IA}{2}\)
Do đó: ΔIFA vuông tại F
=>IF\(\perp\) AD
mà AD//BC
nên \(IF\perp BC\)
c: Xét tứ giác BICD có
BI//CD
BI=CD
Do đó: BICD là hình bình hành
=>BC cắt ID tại trung điểm của mỗi đường
mà E là trung điểm của BC
nên E là trung điểm của ID
=>I,E,D thẳng hàng
31 tháng 10 2022
a: Xét tứ giác ABEF có
BE//AF
BE=AF
BE=BA
Do đó: ABEF là hình thoi
b: Xét ΔBIE có BI=BE
nên ΔBIE cân tại B
mà góc IBE=60 độ
nên ΔBIE đều
=>góc I=60 độ
Xét tứ giác AFEI có
EF//AI
góc I=góc A
Do đó AFEI là hình thang cân
c: Xét ΔBAD có
BF là đường trung tuyến
BF=AD/2
Do đó: ΔBAD vuông tại B
=>DB vuông góc với BI
Xét tứ giác BICD có
BI//CD
BI=CD
Do đó: BICD là hình bình hành
mà DB vuông góc với BI
nên BICD là hình chữ nhật
d: Xét ΔAED có
EF la trung tuyến
FE=DA/2
Do đó: ΔAED vuông tại E
=>góc AED=90 độ
31 tháng 10 2022
a: Xét tứ giác ABEF có
BE//AF
BE=AF
BE=BA
Do đó: ABEF là hình thoi
b: Xét ΔBIE có BI=BE
nên ΔBIE cân tại B
mà góc IBE=60 độ
nên ΔBIE đều
=>góc I=60 độ
Xét tứ giác AFEI có
EF//AI
góc I=góc A
Do đó AFEI là hình thang cân
c: Xét ΔBAD có
BF là đường trung tuyến
BF=AD/2
Do đó: ΔBAD vuông tại B
=>DB vuông góc với BI
Xét tứ giác BICD có
BI//CD
BI=CD
Do đó: BICD là hình bình hành
mà DB vuông góc với BI
nên BICD là hình chữ nhật
d: Xét ΔAED có
EF la trung tuyến
FE=DA/2
Do đó: ΔAED vuông tại E
=>góc AED=90 độ
HH
13 tháng 3 2020
a, Ta có :
EC // FD
\(EC=FD=\frac{4}{2}BC=\frac{1}{2}AD\)
=> ECDF là hình bình hành
\(EF=AB=\frac{1}{2}BC\)
=> ECDF là hình thoi
b, \(\widehat{A} =60^o\)
\(\Rightarrow D=120^o\)
\(\Rightarrow\widehat{EDF}=120^o:2=60^o\)
Mà BE // AD
==> BEDA là hình thang cân
c, Xét tam giác AFE : AF = EF --- > góc AFE
BEFA là hình thoi
==> AE là tia phân giác của \(\widehat{BAE}\Rightarrow\widehat{EAF}=30^o\)
Mà EDA = 60o
=> Trong tam giác EAD = 180o = \(\widehat{EAF}+\widehat{ADE}+\widehat{EAD}\)
\(=30^o+60^o+\widehat{EAD}\)
\(\Rightarrow\widehat{AED}=60^o\)
29 tháng 10 2023
a:
\(BE=EC=\dfrac{BC}{2}\)
\(AF=FD=\dfrac{AD}{2}\)
\(AB=CD=\dfrac{AD}{2}\)
Do đó: BE=EC=AF=FD=AB=CD
Xét tứ giác ABEF có
BE//AF
BE=AF
Do đó: ABEF là hình bình hành
Hình bình hành ABEF có BE=BA
nên ABEF là hình thoi
=>BF\(\perp\)AE
b: Xét ΔABF có AB=AF và \(\widehat{BAF}=60^0\)
nên ΔABF đều
=>\(\widehat{AFB}=60^0\)
\(\widehat{BFD}+\widehat{AFB}=180^0\)(hai góc kề bù)
=>\(\widehat{BFD}+60^0=180^0\)
=>\(\widehat{BFD}=120^0=\widehat{CDF}\)
Xét tứ giác BFDC có FD//BC
nên BCDF là hình thang
Hình thang BCDF có \(\widehat{BFD}=\widehat{CDF}\)
nên BCDF là hình thang cân
c:
ΔABF đều
=>BF=AF
=>\(BF=\dfrac{AD}{2}\)
Xét ΔBAD có
BF là đường trung tuyến
\(BF=\dfrac{AD}{2}\)
Do đó: ΔBAD vuông tại B
=>AB\(\perp\)BD
AB=CD
AB=BM
Do đó: CD=BM
Xét tứ giác BMCD có
BM//CD
BM=CD
Do đó: BMCD là hình bình hành
Hình bình hành BMCD có \(\widehat{MBD}=90^0\)
nên BMCD là hình chữ nhật
=>BC cắt MD tại trung điểm của mỗi đường
mà E là trung điểm của BC
nên E là trung điểm của MD
=>M,E,D thẳng hàng
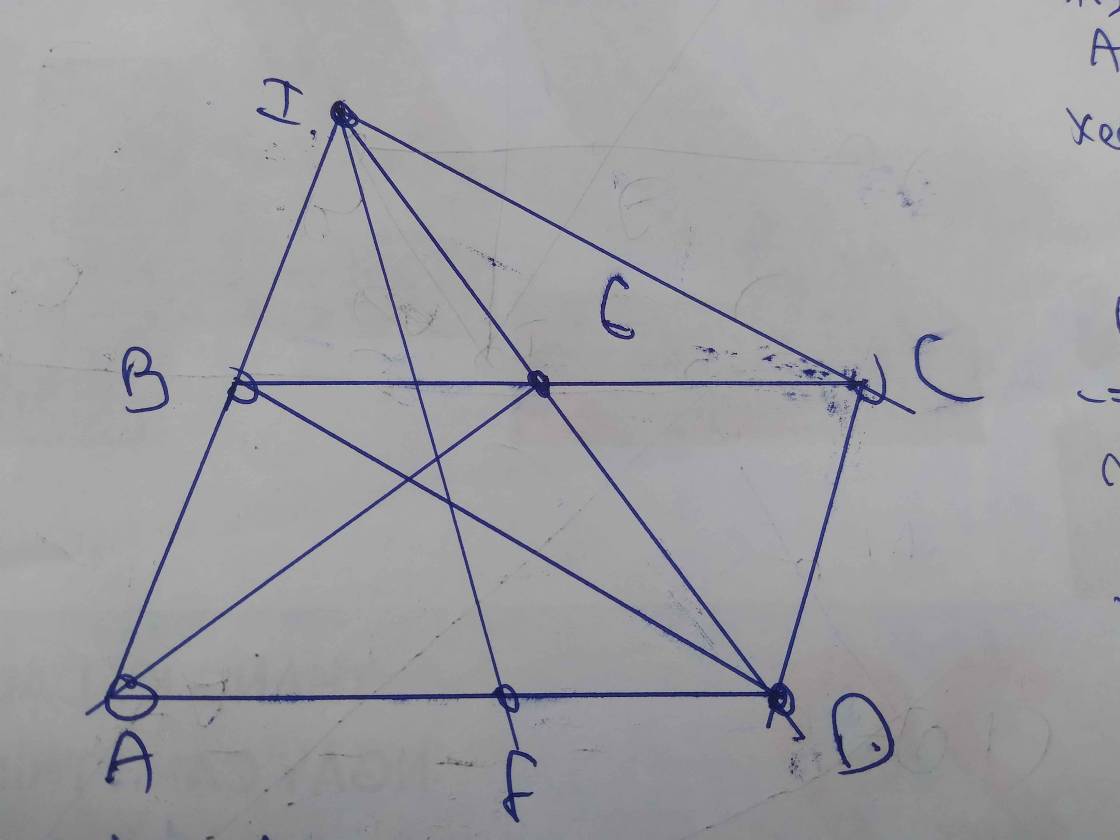
Đề sai bạn nhé. Phải là BD=2AD nhà. Nếu như đề trên thì nó là hình thang chứ ko phải hbh