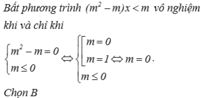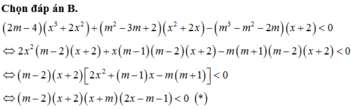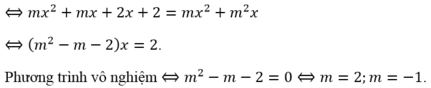Tìm giá trị của tham số m để phương trình mx+2+m2=m2x+3m vô nghiện
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
14 tháng 12 2017
Phương trình ax + b = 0 có nghiệm duy nhất khi a ≠ 0 .
Xét phương trình m 2 + 1 x + 2 = 0 có hệ số a= m2 + 1> 0 với mọi m.
Do đó, phương trình này luôn có nghiệm duy nhất với mọi giá trị của m.
CM
2 tháng 12 2019
Bất phương trình ( m 2 - m ) x < m vô nghiệm khi và chỉ khi m 2 - m = 0 m ≤ 0 ⇔ [ m = 0 m = 1 ⇔ m = 0 m ≤ 0
CM
25 tháng 6 2019
Phương trình ax + b = 0 hoặc ax = b vô nghiệm khi a= 0 và b ≠ 0 .
Xét phương án C:
m m x - 1 = m 2 + 1 x - m ⇔ m 2 x = m 2 x + 1 - m
⇔ 0 x = 1 (vô lí) nên phương trình này vô nghiệm.
Chọn C.
CM
12 tháng 5 2018
Phương trình viết lại m 2 - 4 x = 3 m - 6
Phương trình đã cho vô nghiệm khi m 2 − 4 = 0 3 m − 6 ≠ 0 ⇔ m = ± 2 m ≠ 2 ⇔ m = − 2
Do đó, phương trình đã cho có nghiệm khi m ≠ −2.
Đáp án cần chọn là: B
PT
1
CM
3 tháng 12 2018
Rõ ràng nếu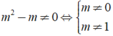
thì bất phương trình luôn có nghiệm.
Với m = 0, bất phương trình trở thành 0x < 0: vô nghiệm.
Với m = 1, bất phương trình trở thành 0x < 1: luôn đúng với mọi x ∈ R
Vậy với m = 0 thì bất phương trình trên vô nghiệm.