giúp mình bài 50 với ạ 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MN
14 tháng 7 2021
Bài 1 :
\(a.\sqrt{x^2-1}\)
\(ĐK:\)
\(x^2-1\ge0\)
\(\Leftrightarrow x^2\ge1\)
\(\Leftrightarrow\left[{}\begin{matrix}x\le-1\\x\ge1\end{matrix}\right.\)
Bài 2 :
\(2\cdot\sqrt{\left(\sqrt{2}-3\right)^2}+\sqrt{48}-5\sqrt{50}\)
\(=2\cdot\left|\sqrt{2}-3\right|+4\sqrt{3}-25\sqrt{2}\)
\(=-2\cdot\left(\sqrt{2}-3\right)+4\sqrt{3}-25\sqrt{2}\)
\(=-2\sqrt{2}-6+4\sqrt{3}-25\sqrt{2}\)
\(=-27\sqrt{2}-6+4\sqrt{3}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
1 tháng 8 2023
Vận tốc của người đi xe máy gấp vận tốc người đi xe đạp số lần là :
60 : 12 = 5 (lần)
Vận tốc của người đi xe máy gấp vận tốc người đi bộ số lần là :
60 : 5 = 12 (lần)
Đáp số :...
HK
3
31 tháng 10 2021
Bạn ơi, làm như vậy thì quá ngắn rồi ạ, với lại bạn làm thiếu mất đề bài của mình rồi
SB
6 tháng 7 2021
mình làm những bài bn chưa lm nhé
9B
10A
bài 2
have repainted
bàii 3
ride - walikking
swimming
watch
22 tháng 3 2022
\(3x=4z\Rightarrow\dfrac{x}{4}=\dfrac{z}{3}\); \(\dfrac{x}{5}=\dfrac{y}{6}\)
\(\Rightarrow\dfrac{x}{20}=\dfrac{z}{15}=\dfrac{y}{24}\)
\(\Rightarrow\dfrac{x}{20}=\dfrac{z}{15}=\dfrac{y}{24}=\dfrac{x-y+z}{20-24+15}=\dfrac{121}{11}=11\)
\(\Rightarrow x=20.11=220;z=15.11=165;y=264\)
13 tháng 10 2023
47 d
48 b
49 a
50 a
đây là theo suy nghĩ của mình thôi nên ko chắc nhé
9 tháng 8 2021
Bài 2:
Ta có:\(2\sqrt{48}< 2\sqrt{49}\) ;
\(3\sqrt{27}>3\sqrt{25}\)
mà \(2\sqrt{49}< 3\sqrt{25}\left(14< 15\right)\)
\(\Rightarrow3\sqrt{27}>3\sqrt{25}>2\sqrt{49}>2\sqrt{48}\)
\(\Rightarrow3\sqrt{27}>2\sqrt{48}\)
b)
Ta có:\(\sqrt{50}+\sqrt{2}>\sqrt{49}+\sqrt{1}\)
\(\sqrt{50+2}< \sqrt{64}\)
mà \(\sqrt{49}+\sqrt{1}=\sqrt{64}\left(8=8\right)\)
\(\Rightarrow\sqrt{50}+\sqrt{2}>8>\sqrt{50+2}\)
\(\Rightarrow\sqrt{50}+\sqrt{2}>\sqrt{50+2}\)
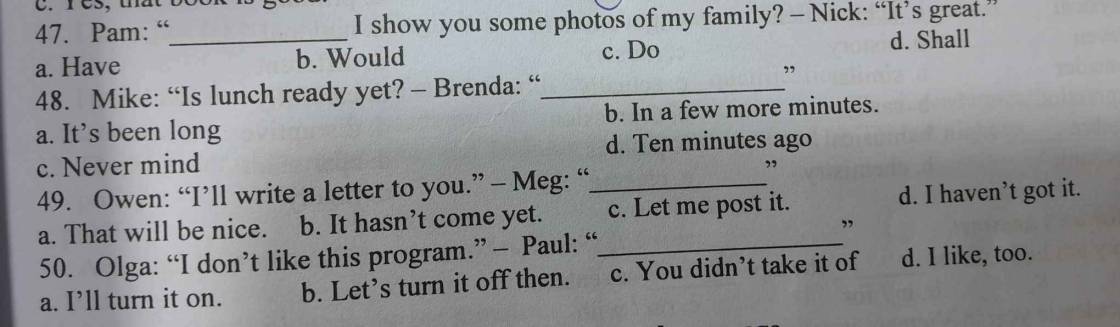
Lời giải:
a. Áp dụng định lý Pitago:
$\sqrt{AB^2-BH^2}=\sqrt{5^2-3^2}=4$ (cm)
$\cos \widehat{ABH}=\frac{BH}{AB}=\frac{3}{5}$
$\Rightarrow \widehat{ABH}=53,13^0$
b.
$\widehat{AMH}=\widehat{ANH}=90^0$
$\Rightarrow \widehat{AMH}+\widehat{ANH}=180^0$
$\Rightarrow AMHN$ là tứ giác nội tiếp
$\Rightarrow \widehat{AMN}=\widehat{AHN}$
Mà $\widehat{AHN}=\widehat{ACB}$ (cùng phụ với $\widehat{NHC}$)
$\Rightarrow \widehat{AMN}=\widehat{ACB}$ (đpcm)
Hình vẽ: