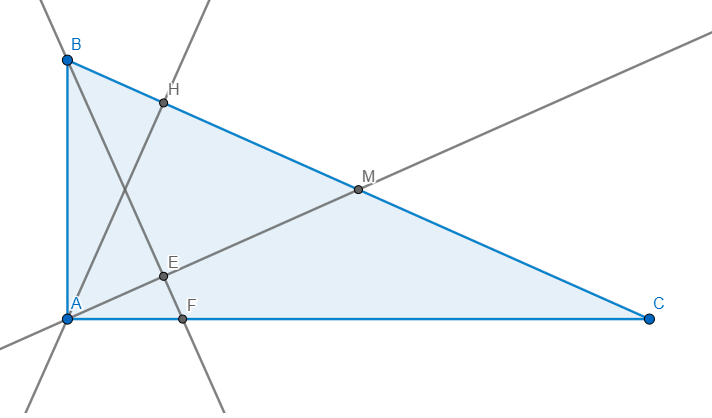
Tam giác ABC vuông tại A , AB < AC , đường cao AH
a) CM: AB2/ AC2 = BH / CH
b) Từ B vẽ đường thẳng vuông góc trung tuyến AM cắt AH tại D ,
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 12 2023
a: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MB=MC
Ta có: MA=MB
=>ΔMAB cân tại M
=>\(\widehat{MAB}=\widehat{MBA}\)
Ta có: \(\widehat{DAB}+\widehat{MAB}=\widehat{DAM}=90^0\)
\(\widehat{HAB}+\widehat{HBA}=90^0\)(ΔHAB vuông tại H)
mà \(\widehat{MAB}=\widehat{HBA}\)(cmt)
nên \(\widehat{DAB}=\widehat{HAB}\)
=>AB là phân giác của góc DAH
21 tháng 3 2023
a: Xét ΔBAD vuông tại A và ΔBHA vuông tại H có
góc ABD chung
=>ΔBAD đồng dạng với ΔBHA
=>BA/BH=BD/BA
=>BA^2=BH*BD
b: Xét ΔAMB có IE//MB
nên IE/MB=AI/AM
Xét ΔAMC có ID//MC
nên ID/MC=AI/AM
=>IE/MB=ID/MC
mà MB=MC
nên IE=ID
=>I là trung điểm của ED
c: DE//BC
=>DI/BM=HI/HM
=>EI/CM=HI/HM
mà góc EIH=góc HMC
nên ΔIEH đồng dạng với ΔMCH
=>góc IHE=góc MHC
=>C,H,E thẳng hàng
AT
13 tháng 7 2021
a) tam giác ABC vuông tại A có AM là trung tuyến \(\Rightarrow AM=\dfrac{BC}{2}\)
Ta có: \(2BH.AM=BH.2AM=BH.BC=AB^2\)
b) tam giác BAF vuông tại A có đường cao AE
\(\Rightarrow BE.BF=BA^2=BH.BC\)
Ta có: \(AM=\dfrac{BC}{2}=BM\Rightarrow\Delta ABM\) cân tại M
\(\Rightarrow\angle MAB=\angle MBA\) mà \(\angle MAB=\angle BFA\Rightarrow\angle ABC=\angle BFA\)
Xét \(\Delta ABF\) và \(\Delta ACB:\) Ta có: \(\left\{{}\begin{matrix}\angle BACchung\\\angle ABC=\angle BFA\end{matrix}\right.\)
\(\Rightarrow\Delta ABF\sim\Delta ACB\left(g-g\right)\Rightarrow\dfrac{AB}{AC}=\dfrac{AF}{AB}\Rightarrow AB^2=AF.AC\)
\(\Rightarrow BE.BF=BH.BC=AF.AC\)
