B=[(3x-2)(x+1)-(2x+5)(x^2-1)]:(x+1)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 10 2021
a: Ta có: \(\left(x^2-2x+2\right)\left(x^2-2\right)\left(x^2+2x+2\right)\left(x^2+2\right)\)
\(=\left(x^4-4\right)\left[\left(x^2+2\right)^2-4x^2\right]\)
\(=\left(x^4-4\right)\left(x^4+4x^2+4-4x^2\right)\)
\(=\left(x^4-4\right)\cdot\left(x^4+4\right)\)
\(=x^8-16\)
b: Ta có: \(\left(x+1\right)^2-\left(x-1\right)^2+3x^2-3x\left(x+1\right)\left(x-1\right)\)
\(=x^2+2x+1-x^2+2x-1+3x^2-3x\left(x^2-1\right)\)
\(=3x^2+4x-3x^3+3x\)
\(=-3x^3+3x^2+7x\)
3 tháng 2 2021
a) Ta có: \(x^2-3x+7=1+2x\)
\(\Leftrightarrow x^2-3x+7-1-2x=0\)
\(\Leftrightarrow x^2-3x-2x+6=0\)
\(\Leftrightarrow x\left(x-3\right)-2\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\end{matrix}\right.\)
Vậy: S={3;2}
b) Ta có: \(x^2-3x-10=0\)
\(\Leftrightarrow x^2-5x+2x-10=0\)
\(\Leftrightarrow x\left(x-5\right)+2\left(x-5\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-5=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-2\end{matrix}\right.\)
Vậy: S={5;-2}
c) Ta có: \(x^2-3x+4=2\left(x-1\right)\)
\(\Leftrightarrow x^2-3x+4=2x-2\)
\(\Leftrightarrow x^2-3x+4-2x+2=0\)
\(\Leftrightarrow x^2-3x-2x+6=0\)
\(\Leftrightarrow x\left(x-3\right)-2\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\end{matrix}\right.\)
Vậy: S={3;2}
d) Ta có: \(\left(x+1\right)\left(x-2\right)\left(x-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\x-2=0\\x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=2\\x=5\end{matrix}\right.\)
Vậy: S={-1;2;5}
e) Ta có: \(2x^2+3x+1=0\)
\(\Leftrightarrow2x^2+2x+x+1=0\)
\(\Leftrightarrow2x\left(x+1\right)+\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\2x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\2x=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{-1}{2}\end{matrix}\right.\)
Vậy: \(S=\left\{-1;\dfrac{-1}{2}\right\}\)
f) Ta có: \(4x^2-3x=2x-1\)
\(\Leftrightarrow4x^2-3x-2x+1=0\)
\(\Leftrightarrow4x^2-5x+1=0\)
\(\Leftrightarrow4x^2-4x-x+1=0\)
\(\Leftrightarrow4x\left(x-1\right)-\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(4x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\4x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\4x=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{4}\end{matrix}\right.\)
Vậy: \(S=\left\{1;\dfrac{1}{4}\right\}\)
P
1
2 tháng 2 2024
b: 2x+5=x-5
=>2x-x=-5-5
=>x=-10
c: 2x(x+2)+5(x-2)=0
=>\(2x^2+4x+5x-10=0\)
=>\(2x^2+9x-10=0\)
\(\text{Δ}=9^2-4\cdot2\cdot\left(-10\right)=81+80=161>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-9-\sqrt{161}}{4}\\x_2=\dfrac{-9+\sqrt{161}}{4}\end{matrix}\right.\)
h:
ĐKXĐ: \(x\notin\left\{2;-1\right\}\)
\(\dfrac{2}{x+1}-\dfrac{1}{x-2}=\dfrac{3x-11}{\left(x+1\right)\left(x-2\right)}\)
=>\(\dfrac{2\left(x-2\right)-\left(x+1\right)}{\left(x-2\right)\left(x+1\right)}=\dfrac{3x-11}{\left(x+1\right)\left(x-2\right)}\)
=>\(2\left(x-2\right)-\left(x+1\right)=3x-11\)
=>2x-4-x-1=3x-11
=>x-5=3x-11
=>x-3x=-11+5
=>-2x=-6
=>x=3(nhận)
i: 3x-12=0
=>3x=12
=>x=12/3=4
f: \(\dfrac{x-3}{5}+\dfrac{1+2x}{3}=6\)
=>\(\dfrac{3\left(x-3\right)+5\left(2x+1\right)}{15}=6\)
=>\(\dfrac{3x-9+10x+5}{15}=6\)
=>13x-4=90
=>13x=94
=>\(x=\dfrac{94}{13}\)
26 tháng 3 2020
a) (3x + 1)^2 - 2(3x + 1)(3x - 5) + (3x - 5)^2
= 9x^2 + 6x + 1 - 18x^2 + 24x + 10 + 9x^2 - 30x + 25
= 36
b) (3x^2 - y)^2
= 9x^4 - 6x^2y + y^2
c) (3x + 5)^2 + (3x - 5)^2 - (3x + 2)(3x - 2)
= 9x^2 + 30x + 25 + 9x^2 - 30x + 25 - 9x^2 + 4
= 9x^2 + 54
d) 2x(2x - 1)^2 - 3x(x + 3)(x - 3) - 4x(x + 1)^2
= 8x^3 - 8x^2 + 2x - 3x^2 + 27x - 4x^3 - 8x^2 - 4x
= x^3 - 16x^2 + 25x
e) (x - 2)(x^2 + 2x + 4) - (x + 1)^2 + 3(x - 1)(x + 1)
= x^3 - 8 - x^2 - 2x - 1 + 3x^2 - 2
= x^3 + 2x^2 - 2x - 12
f) (x^4 - 5x^2 + 25)(x^2 + 5) - (2 + x^2)^2 + 3(1 + x^2)^2
= x^6 + 125 - 4 - 4x^2 - x^2 + 3 + 6x^2 + 3x^4
= x^6 + 2x^4 + 2x^2 + 124
10 tháng 11 2021
\(A=2x^3+3x^2-3-5x^2-5x=2x^3-2x^2-5x-3\\ B=125-150x+60x^2-8x^3-25+9x^2=-8x^3+69x^2-150x+100\\ C=\left(3x+1-2x+1\right)\left(3x+1+2x-1\right)=5x\left(x+2\right)=5x^2+10x\\ D=\left(2x+1-3+x\right)^2=\left(3x-2\right)^2=9x^2-12x+4\\ E=x^3-6x^2+12x-8-x^3+x+6x^2-18x=-5x-8\\ F=x^3-3x^2+3x-1-3+3x^2-x^3+1-3x=-3\)
MN
17 tháng 2 2020
a) \(\left(3x-1\right)\left(x+3\right)=\left(2-x\right)\left(5-3x\right)\)
\(\Leftrightarrow3x^2+8x-3=3x^2-11x+10\)
\(\Leftrightarrow19x-13=0\)
\(\Leftrightarrow x=\frac{13}{19}\)
Vậy tập nghiệm của phương trình là \(S=\left\{\frac{13}{19}\right\}\)
b) \(\left(x+5\right)\left(2x-1\right)=\left(2x-3\right)\left(x+1\right)\)
\(\Leftrightarrow2x^2+9x-5=2x^2-x-3\)
\(\Leftrightarrow10x-2=0\)
\(\Leftrightarrow x=\frac{1}{5}\)
Vậy tập nghiệm của phương trình là \(S=\left\{\frac{1}{5}\right\}\)
c) \(\left(x+1\right)\left(x+9\right)=\left(x+3\right)\left(x+5\right)\)
\(\Leftrightarrow x^2+10x+9=x^2+8x+15\)
\(\Leftrightarrow2x-6=0\)
\(\Leftrightarrow x=3\)
Vậy tập nghiệm của phương trình là \(S=\left\{3\right\}\)
MN
17 tháng 2 2020
d) \(\left(3x+5\right)\left(2x+1\right)=\left(6x-2\right)\left(x-3\right)\)
\(\Leftrightarrow6x^2+13x+5=6x^2-20x+6\)
\(\Leftrightarrow33x-1=0\)
\(\Leftrightarrow x=\frac{1}{33}\)
Vậy tập nghiệm của phương trình là \(S=\left\{\frac{1}{33}\right\}\)
e) \(\left(x+2\right)^2+2\left(x-4\right)=\left(x-4\right)\left(x-2\right)\)
\(\Leftrightarrow x^2+4x+4+2x-8=x^2-6x+8\)
\(\Leftrightarrow6x-4=-6x+8\)
\(\Leftrightarrow12x-12=0\)
\(\Leftrightarrow x=1\)
Vậy tập nghiệm của phương trình là \(S=\left\{1\right\}\)
f) \(\left(x+1\right)\left(2x-3\right)-\left(3x-2\right)=2\left(x-1\right)^2\)
\(\Leftrightarrow2x^2-x-3-3x+2=2\left(x^2-2x+1\right)\)
\(\Leftrightarrow2x^2-4x-1=2x^2-4x+2\)
\(\Leftrightarrow-1=2\)(ktm)
Vậy tập nghiệm của phương trình là \(S=\varnothing\)
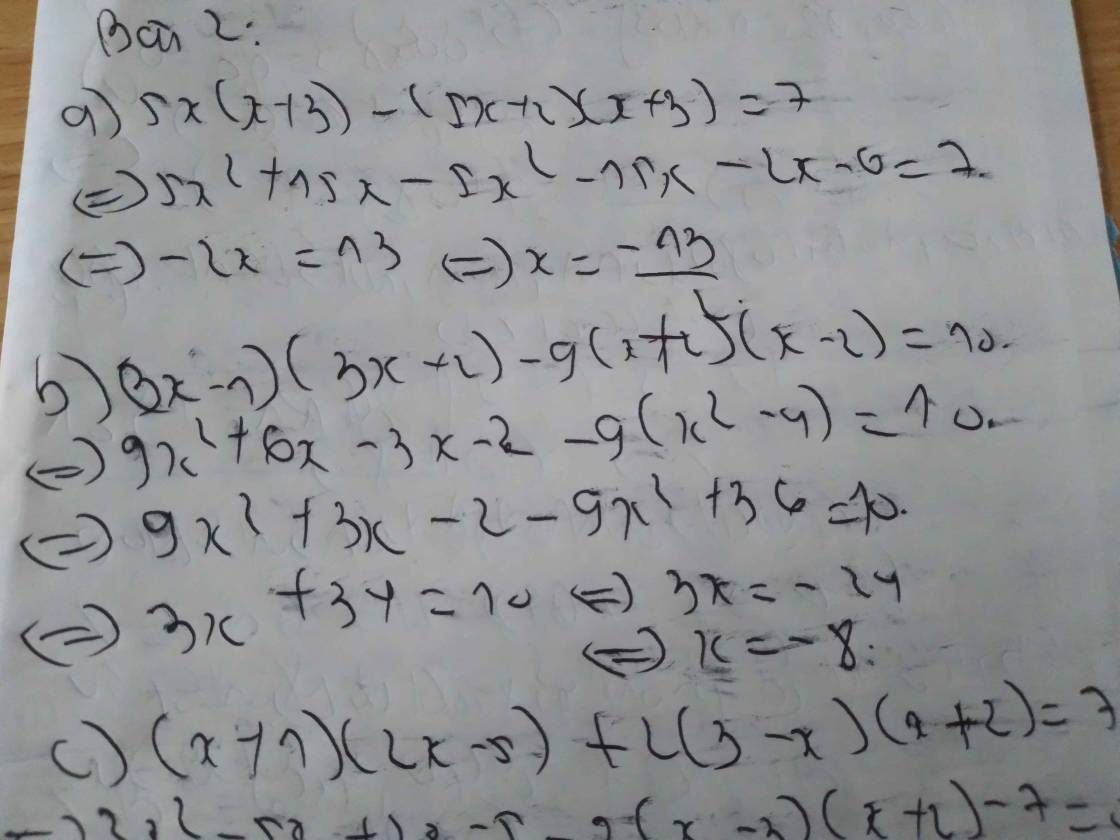
\(B=\left(3x-2\right)\left(x+1\right):\left(x+1\right)-\left(2x+5\right)\left(x-1\right)\left(x+1\right):\left(x+1\right)\)
\(=\left(3x+2\right)-\left(2x+5\right)\left(x-1\right)\)
Em tiếp tục phân tích rồi rút gọn nhé!