cho \(x^2-y^2=1\)
tính A=\(2\left(x^6-y^6\right)-3\left(x^4+y^4\right)\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 7 2021
a.
\(\left\{{}\begin{matrix}x^4+y^4=34\\y=2-x\end{matrix}\right.\)
\(\Rightarrow x^4+\left(x-2\right)^4=34\)
Đặt \(x-1=t\)
\(\Rightarrow\left(t+1\right)^4+\left(t-1\right)^4=34\)
\(\Leftrightarrow t^4+6t^2-16=0\Rightarrow\left[{}\begin{matrix}t^2=2\\t^2=-8\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}t=\sqrt{2}\Rightarrow x=\sqrt{2}+1\Rightarrow y=1-\sqrt{2}\\t=-\sqrt{2}\Rightarrow x=1-\sqrt{2}\Rightarrow y=1+\sqrt{2}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 7 2021
b.
\(\left\{{}\begin{matrix}xy^2-x^2y+6x-y^2-y-6=0\\x^2y-xy^2+6y-x^2-x-6=0\end{matrix}\right.\) (1)
Lần lượt cộng 2 vế và trừ 2 vế ta được:
\(\left\{{}\begin{matrix}-x^2-y^2+5x+5y-12=0\\2xy\left(y-x\right)+7\left(x-y\right)+\left(x-y\right)\left(x+y\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+y^2-5\left(x+y\right)+12=0\\\left(y-x\right)\left(2xy-x-y-7\right)=0\end{matrix}\right.\)
Th1: \(\left\{{}\begin{matrix}x=y\\x^2+y^2-5\left(x+y\right)+12=0\end{matrix}\right.\)
\(\Rightarrow2x^2-10x+12=0\Rightarrow...\)
TH2: \(\left\{{}\begin{matrix}2xy-\left(x+y\right)-7=0\\x^2+y^2-5\left(x+y\right)+12=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2xy-\left(x+y\right)-7=0\\\left(x+y\right)^2-2xy-5\left(x+y\right)+12=0\end{matrix}\right.\)
Đặt \(\left\{{}\begin{matrix}x+y=u\\xy=v\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2v-u-7=0\\u^2-2v-5u+12=0\end{matrix}\right.\)
\(\Rightarrow u^2-6u+5=0\)
\(\Leftrightarrow...\)
PT
2
S
12 tháng 8 2021
Đây nè bạn. Mk chỉ mới nghĩ ra cách này thôi à!!! Bạn nào có cách nào thì bảo mk với nhé!!!
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 8 2021
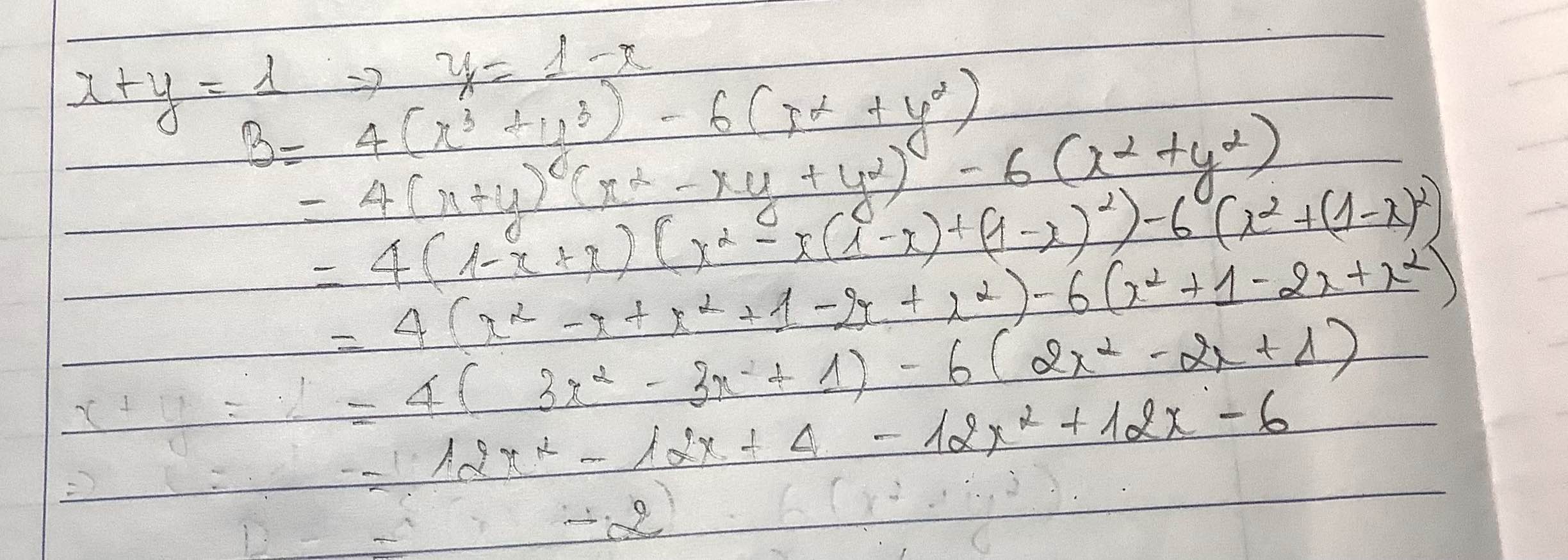
\(B=4\left(x+y\right)\left(x^2+y^2-xy\right)-6\left[\left(x+y\right)^2-2xy\right]\)
\(=4\left[\left(x+y\right)^2-3xy\right]-6\left(1-2xy\right)\)
\(=4-12xy-6+12xy\)
\(=-2\)
H9
HT.Phong (9A5)
CTVHS
19 tháng 10 2023
a) \(\left(x-2y\right)\left(3xy+6x^2+x\right)\)
\(=x\left(3xy+6x^2+x\right)-2y\left(3xy+6x^2+x\right)\)
\(=3x^2y+6x^3+x^2-6xy^2-12x^2y-2xy\)
\(=6x^3+x^2-9x^2y-6xy^2-2xy\)
b) \(\left(18x^4y^3-24x^3y^4+12x^3y^3\right):\left(-6x^2y^3\right)\)
\(=18x^4y^3:\left(-6x^2y^3\right)-24x^3y^4:\left(-6x^2y^3\right)+12x^3y^3:\left(-6x^2y^3\right)\)
\(=-3x^2+4xy-2x\)
VQ
26 tháng 10 2023
a) (�−2�)(3��+6�2+�)(x−2y)(3xy+6x2+x)
=�(3��+6�2+�)−2�(3��+6�2+�)=x(3xy+6x2+x)−2y(3xy+6x2+x)
=3�2�+6�3+�2−6��2−12�2�−2��=3x2y+6x3+x2−6xy2−12x2y−2xy
=6�3+�2−9�2�−6��2−2��=6x3+x2−9x2y−6xy2−2xy
b) (18�4�3−24�3�4+12�3�3):(−6�2�3)(18x4y3−24x3y4+12x3y3):(−6x2y3)
=18�4�3:(−6�2�3)−24�3�4:(−6�2�3)+12�3�3:(−6�2�3)=18x4y3:(−6x2y3)−24x3y4:(−6x2y3)+12x3y3:(−6x2y3)
=−3�2+4��−2�=−3x2+4xy−2x
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 4 2021
a. Làm gọn 1 chút xíu:
\(y=\left(x^{11}+2x^7-3x^5-6x\right)\left(3x^7+6x^2-2\right)\)
\(y'=\left(11x^{10}+14x^6-15x^4-6\right)\left(3x^7+6x^2-2\right)+\left(21x^6+12x\right)\left(x^{11}+2x^7-3x^5-6x\right)\)
b.
\(y'=5\left(x^4-\dfrac{2}{3x}\right)^4\left(4x^3+\dfrac{2}{3x^2}\right)\Rightarrow y'\left(10\right)=5\left(10^4-\dfrac{2}{30}\right)^4\left(4.10^3+\dfrac{2}{300}\right)=?\)
c.
\(y'=\dfrac{7}{\left(x+1\right)^2}\Rightarrow y'\left(4\right)=\dfrac{7}{25}\)
PT
Phạm Trần Hoàng Anh
CTVHS
20 tháng 9 2021
a, Với x = 3 và y = -2 ta có:
\(A=\dfrac{3}{2}+\dfrac{4}{9}.\left(6-\left|3\right|\right)+\left(-2\right)\)
\(A=\dfrac{3}{2}+\dfrac{4}{9}.\left(6-3\right)-2\)
\(A=\dfrac{3}{2}+\dfrac{4}{9}.3-2\)
\(A=\dfrac{3}{2}+\dfrac{4}{3}-2\)
\(A=\dfrac{5}{6}\)
Với x = 3 và y = -3 ta có:
\(B=\left|2.3-1\right|+\left|3.\left(-3\right)+2\right|\)
\(B=\left|5\right|+\left|-7\right|\)
\(B=5+7=12\)
Hoctot ! ko hiểu chỗ nào cứ hỏi cj nhé
4 tháng 8 2022
a: Đặt |x-6|=a, |y+1|=b
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}2a+3b=5\\5a-4b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=1\end{matrix}\right.\)
=>|x-6|=1 và |y+1|=1
\(\Leftrightarrow\left\{{}\begin{matrix}x\in\left\{7;5\right\}\\y\in\left\{0;-2\right\}\end{matrix}\right.\)
b: Đặt |x+y|=a, |x-y|=b
Theo đề, ta có: \(\left\{{}\begin{matrix}2a-b=19\\3a+2b=17\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{55}{7}\\b=-\dfrac{23}{7}\left(loại\right)\end{matrix}\right.\)
=>HPTVN
c: Đặt |x+y|=a, |x-y|=b
Theo đề ta có: \(\left\{{}\begin{matrix}4a+3b=8\\3a-5b=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=0\end{matrix}\right.\)
=>|x+y|=2 và x=y
=>|2x|=2 và x=y
=>x=y=1 hoặc x=y=-1
Ta có x2 - y2 = 1
=> (x2-y2)3 = 13
=> x6 - 3x4y2 + 3x2y4 - x6 = 1
=> x6-y6 -3x2y2 (x2-y2) =1 mà x2-y2 =1
=> x6 - y6 -3x2y2 = 1 => x6-y6 = 1+ 3x2y2 (1)
Ta lại có : x2 - y2 =1
=> (x2 -y2)2 = 12
=> x4 -2x2y2 + y4 =1 => x4 + y4 = 1+ 2x2y2 (2)
Từ (1), (2) thay vào A ta có
A= 2( 1+ 3x2y2 ) -3( 1+2x2y2) = 2+6x2y2 - 3 - 6x2y2 = -1
Có thể tham khảo thêm 1 cách khác nhé!
Câu hỏi của Lãnh Hàn Thần - Toán lớp 8 - Học toán với OnlineMath