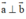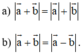Chờ 2 vecto a và b khác vectơ 0. Đẳng thức |a+b|=|a-b| xảy ra khi hai vecto a và b như nào
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giả thiết => cos \(\left(\overrightarrow{a};\overrightarrow{b}\right)=\dfrac{1}{2}\)
⇒ \(\left(\overrightarrow{a};\overrightarrow{b}\right)=60^0\)

\(\cos\left(\overrightarrow{a},\overrightarrow{b}\right)=\dfrac{\left(-1\right)\cdot2+1\cdot0}{\sqrt{\left(-1\right)^2+1^2}+\sqrt{2^2+0^2}}=-2+\sqrt{2}\)
\(\Leftrightarrow\left(\overrightarrow{a},\overrightarrow{b}\right)=125^0\)

Phương án A sai vì có thể xảy ra trường hợp giống câu 4 như hình sau:

Phương án B và C sai vì có thể sảy ra như hình sau.

Phương án D đúng vì: có thể ba vecto n → , a → , b → đồng phẳng hoặc không đồng phẳng như hai hình trên.
Đáp án D

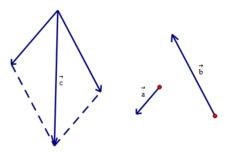
a → , b → , c → đồng phẳng vì a → và b → không cùng phương và có cặp số (2; -1) sao cho c → = 2 a → - b →

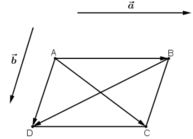
Có hai vec tơ a→, b→ bất kì như hình vẽ.
Vẽ hình bình hành ABCD sao cho 
Ta có:
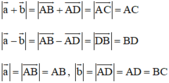
Do đó
a) 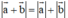 ⇔ AC = AB + BC ⇔ B nằm giữa A và C
⇔ AC = AB + BC ⇔ B nằm giữa A và C
⇔ 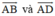 cùng hướng hay a→ và b→ cùng hướng.
cùng hướng hay a→ và b→ cùng hướng.
b) 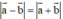 ⇔ AC = BD
⇔ AC = BD
⇔ ABCD là hình chữ nhật
⇔ AB ⊥ CD hay