\(\sqrt{ 6-\sqrt{11} } -\sqrt{ 6+\sqrt{11} }\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 10 2023
a: \(\left(3+\sqrt{2}\right)^2=3^2+2\cdot3\cdot\sqrt{2}+\left(\sqrt{2}\right)^2\)
\(=9+6\sqrt{2}+2=11+6\sqrt{2}\)
b: \(\sqrt{11+6\sqrt{2}}+\sqrt{11-6\sqrt{2}}\)
\(=\sqrt{\left(3+\sqrt{2}\right)^2}+\sqrt{\left(3-\sqrt{2}\right)^2}\)
\(=3+\sqrt{2}+3-\sqrt{2}=6\)
c: \(\sqrt{8-2\sqrt{7}}-\sqrt{8+2\sqrt{7}}\)
\(=\sqrt{\left(\sqrt{7}-1\right)^2}-\sqrt{\left(\sqrt{7}+1\right)^2}\)
\(=\sqrt{7}-1-\sqrt{7}-1=-2\)
d: \(\sqrt{49-12\sqrt{5}}-\sqrt{49+12\sqrt{5}}\)
\(=\sqrt{45-2\cdot3\sqrt{5}\cdot2+4}-\sqrt{45+2\cdot3\sqrt{5}\cdot2+4}\)
\(=\sqrt{\left(3\sqrt{5}-2\right)^2}-\sqrt{\left(3\sqrt{5}+2\right)^2}\)
\(=3\sqrt{5}-2-3\sqrt{5}-2=-4\)
MH
12 tháng 10 2023
a) \(\left(3+\sqrt{2}\right)^2=9+6\sqrt{2}+2=11+6\sqrt{2}\)
b) \(\sqrt{11+6\sqrt{2}}+\sqrt{11-6\sqrt{2}}\)
\(=\sqrt{\left(3+\sqrt{2}\right)^2}+\sqrt{\left(3-\sqrt{2}\right)^2}\)
\(=3+\sqrt{2}+3-\sqrt{2}=6\)
c) \(\sqrt{8-2\sqrt{7}}-\sqrt{8+2\sqrt{7}}\)
\(=\sqrt{\left(\sqrt{7}-1\right)^2}-\sqrt{\left(\sqrt{7}+1\right)^2}\)
\(=\sqrt{7}-1-\sqrt{7}-1=-2\)
d) \(\sqrt{49-12\sqrt{5}}-\sqrt{49+12\sqrt{5}}\)
\(=\sqrt{\left(3\sqrt{5}-2\right)^2}-\sqrt{\left(3\sqrt{5}+2\right)^2}\)
\(=3\sqrt{5}-2-3\sqrt{5}-2=-4\)
27 tháng 7 2023
b: =căn 10-3+4-căn 10=1
a: \(=\sqrt{11-4\sqrt{6}+\sqrt{15}}\)
H9
HT.Phong (9A5)
CTVHS
24 tháng 8 2023
a) \(\sqrt{6-\sqrt{11}}\cdot\sqrt{6+\sqrt{11}}\)
\(=\sqrt{\left(6-\sqrt{11}\right)\left(6+\sqrt{11}\right)}\)
\(=\sqrt{6^2-\left(\sqrt{11}\right)^2}\)
\(=\sqrt{36-11}\)
\(=\sqrt{25}\)
\(=\sqrt{5^2}\)
\(=5\)
b) \(\sqrt{8+\sqrt{15}}\cdot\sqrt{8-\sqrt{15}}\)
\(=\sqrt{\left(8+\sqrt{15}\right)\left(8-\sqrt{15}\right)}\)
\(=\sqrt{8^2-\left(\sqrt{15}\right)^2}\)
\(=\sqrt{64-15}\)
\(=\sqrt{49}\)
\(=\sqrt{7^2}\)
\(=7\)
24 tháng 8 2023
a: \(=\sqrt{6^2-11}=\sqrt{25}=5\)
b: \(=\sqrt{8^2-15}=\sqrt{49}=7\)
H9
HT.Phong (9A5)
CTVHS
10 tháng 9 2023
Ta có VT:
\(VT=\sqrt{11+6\sqrt{2}}+\sqrt{11-6\sqrt{2}}\)
\(=\sqrt{3^2+2\cdot3\cdot\sqrt{2}+\left(\sqrt{2}\right)^2}+\sqrt{3^2-2\cdot3\cdot\sqrt{2}+\left(\sqrt{2}\right)^2}\)
\(=\sqrt{\left(3+\sqrt{2}\right)^2}+\sqrt{\left(3-\sqrt{2}\right)^2}\)
\(=\left|3+\sqrt{2}\right|+\left|3-\sqrt{2}\right|\)
\(=3+\sqrt{2}+3-\sqrt{2}\)
\(=6=VP\left(dpcm\right)\)
10 tháng 9 2023
\(VT=\sqrt{9+2\cdot3\cdot\sqrt{2}+2}+\sqrt{9-2\cdot3\cdot\sqrt{2}+2}\)
\(=3+\sqrt{2}+3-\sqrt{2}\)
=6=VP
AH
Akai Haruma
Giáo viên
4 tháng 9 2023
Lời giải:
a. \(=|\sqrt{7}-5|+|2-\sqrt{7}|=5-\sqrt{7}+(\sqrt{7}-2)=3\)
b. \(=\sqrt{(3+\sqrt{2})^2}-\sqrt{(3-\sqrt{2})^2}=|3+\sqrt{2}|-|3-\sqrt{2}|\)
\(=(3+\sqrt{2})-(3-\sqrt{2})=2\sqrt{2}\)
c.
\(=\sqrt{(3+2\sqrt{2})^2}+\sqrt{(3-2\sqrt{2})^2}=|3+2\sqrt{2}|+|3-2\sqrt{2}|\)
$=(3+2\sqrt{2})+(3-2\sqrt{2})=6$
d.
$=\sqrt{(\sqrt{5}+1)^2}-\sqrt{(\sqrt{5}-1)^2}$
$=|\sqrt{5}+1|-|\sqrt{5}-1|=\sqrt{5}+1-(\sqrt{5}-1)=2$
27 tháng 8 2021
\(\sqrt{11+6\sqrt{2}}-\sqrt{11-6\sqrt{2}}\)
\(=3+\sqrt{2}-3+\sqrt{2}\)
\(=2\sqrt{2}\)
L
3
21 tháng 10 2021
\(A=\sqrt{6-\sqrt{11}}-\sqrt{6+\sqrt{11}}=\dfrac{\sqrt{2}\left(\sqrt{6-\sqrt{11}}-\sqrt{6+\sqrt{11}}\right)}{\sqrt{2}}=\dfrac{\sqrt{12-2\sqrt{11}}-\sqrt{12+2\sqrt{11}}}{\sqrt{2}}=\dfrac{\sqrt{\left(\sqrt{11}-1\right)^2}-\sqrt{\left(\sqrt{11}+1\right)^2}}{\sqrt{2}}=\dfrac{\sqrt{11}-1-\sqrt{11}-1}{\sqrt{2}}=\dfrac{-2}{\sqrt{2}}=-\sqrt{2}\)
21 tháng 10 2021
\(A=\sqrt{\left(\sqrt{\dfrac{11}{2}}-\sqrt{\dfrac{1}{2}}\right)^2}-\sqrt{\left(\dfrac{11}{2}+\sqrt{\dfrac{1}{2}}\right)^2}\\ A=\sqrt{\dfrac{11}{2}}-\sqrt{\dfrac{1}{2}}-\sqrt{\dfrac{11}{2}}-\sqrt{\dfrac{1}{2}}\\ A=-2\sqrt{\dfrac{1}{2}}=-\dfrac{2\sqrt{2}}{2}=-\sqrt{2}\)
19 tháng 8 2021
Ta có: \(6\sqrt{2}+\sqrt{6-\sqrt{11}}-\sqrt{6+\sqrt{11}}\)
\(=\dfrac{12+\sqrt{12-2\sqrt{11}}-\sqrt{12+2\sqrt{11}}}{\sqrt{2}}\)
\(=\dfrac{12+\sqrt{11}-1-\sqrt{11}-1}{\sqrt{2}}\)
\(=5\sqrt{2}\)
AH
Akai Haruma
Giáo viên
26 tháng 8 2023
Lời giải:
a.
\(=\sqrt{5+2.2\sqrt{5}+2^2}-\sqrt{5-2.2\sqrt{5}+2^2}\)
$=\sqrt{(\sqrt{5}+2)^2}-\sqrt{(\sqrt{5}-2)^2}$
$=|\sqrt{5}+2|-|\sqrt{5}-2|=(\sqrt{5}+2)-(\sqrt{5}-2)=4$
b.
$=\sqrt{3-2.3\sqrt{3}+3^2}+\sqrt{3+2.3.\sqrt{3}+3^2}$
$=\sqrt{(\sqrt{3}-3)^2}+\sqrt{(\sqrt{3}+3)^2}$
$=|\sqrt{3}-3|+|\sqrt{3}+3|$
$=(3-\sqrt{3})+(\sqrt{3}+3)=6$
c.
$=\sqrt{2+2.3\sqrt{2}+3^2}-\sqrt{2-2.3\sqrt{2}+3^2}$
$=\sqrt{(\sqrt{2}+3)^2}-\sqrt{(\sqrt{2}-3)^2}$
$=|\sqrt{2}+3|-|\sqrt{2}-3|$
$=(\sqrt{2}+3)-(3-\sqrt{2})=2\sqrt{2}$
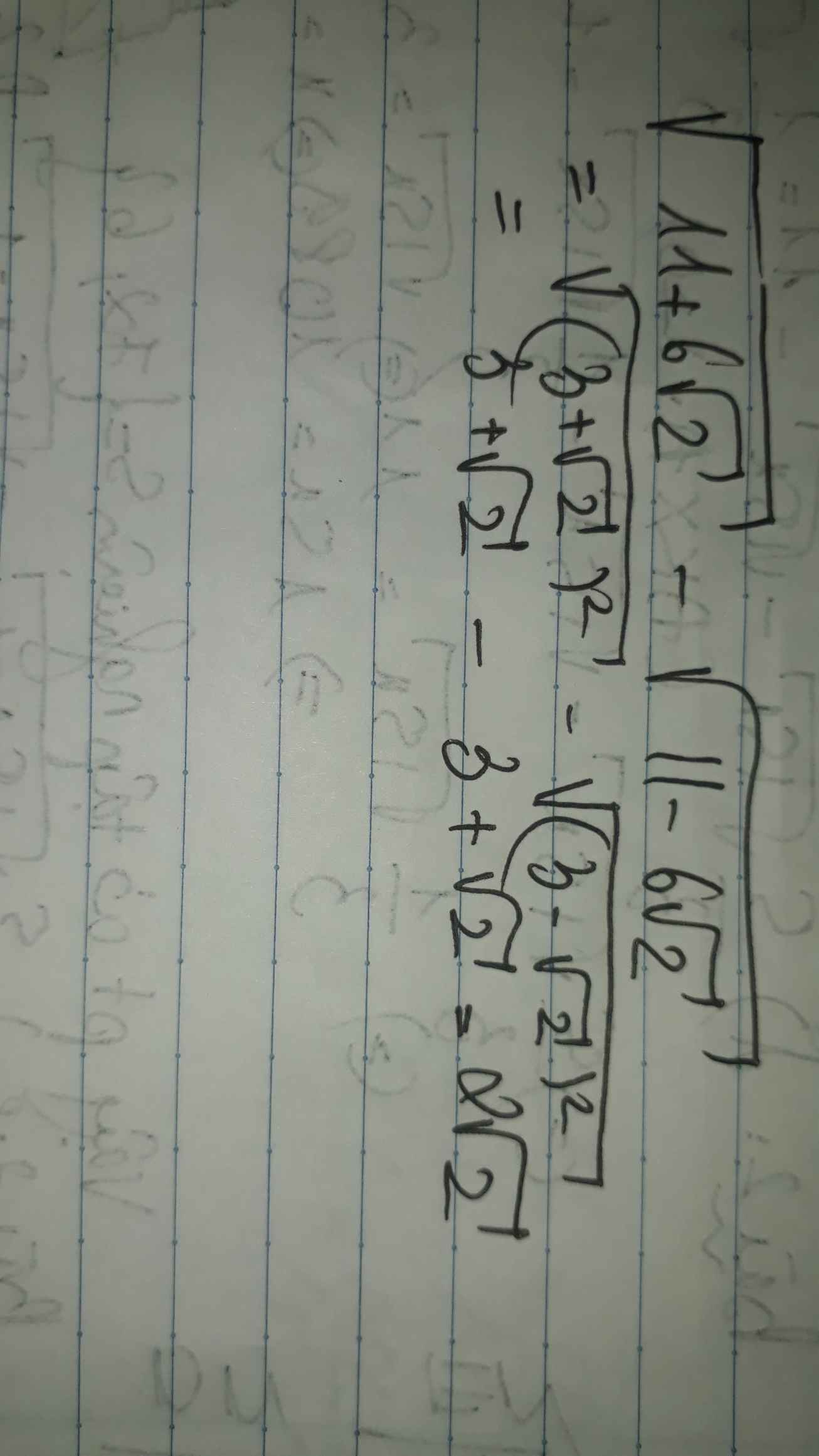
Đặt \(A=\sqrt{6-\sqrt{11}}-\sqrt{6+\sqrt{11}}\)
\(\Rightarrow A^2=6-\sqrt{11}-2\sqrt{\left(6-\sqrt{11}\right)\left(6+\sqrt{11}\right)}+6+\sqrt{11}\)
\(\Leftrightarrow A^2=12-2\sqrt{36-11}\)
\(\Leftrightarrow A^2=12-2.\sqrt{25}\)
\(\Leftrightarrow A^2=2\)(1)
Vì \(\hept{\begin{cases}\sqrt{6-\sqrt{11}}>0\\\sqrt{6+\sqrt{11}}>0\end{cases}}\)và \(6-\sqrt{11}< 6+\sqrt{11}\)
\(\Rightarrow A=\sqrt{6-\sqrt{11}}-\sqrt{6+\sqrt{11}}< 0\)(2)
Từ(1),(2) \(\Rightarrow A=-\sqrt{2}\)