Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
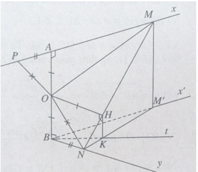
Theo giả thiết ta có M và N là hai điểm di động lần lượt trên hai tia Ax và By sao cho AM + BN = MN.
a) Kéo dài MA một đoạn AP = BN, ta có MP = MN và OP = ON.
Do đó ΔOMP = ΔOMN (c.c.c)
⇒ OA = OH nên OH = a.
Ta suy ra HM = AM và HN = BN.
b) Gọi M’ là hình chiếu vuông góc của điểm M trên mặt phẳng (Bx’, By) ta có:
HK // MM’ với K ∈ NM’.
Do đó đối với tam giác BNM’ đường thẳng BK là phân giác của góc (x'By) .
c) Gọi (β) là mặt phẳng (AB, BK). Vì HK // AB nên HK nằm trong mặt phẳng (β) và do đó H thuộc mặt phẳng (β). Trong mặt phẳng (β) ta có OH = a. Vậy điểm H luôn luôn nằm trên đường tròn cố định, đường kính AB và nằm trong mặt phẳng cố định (β) = (AB, BK)
a: ΔABC vuông cân tại A có AH là đường cao
nên H là trung điểm của BC
Xét ΔCAB có CH/CB=CM/CA=1/2
nên HM//AB và HM/AB=CH/CB=1/2
=>HM=1/2AB
c: Xét ΔCDB có
CA,BN là đường cao
CA cắt BN tại M
=>M là trực tâm
=>DM vuông góc BC
=>góc MDB=90-45=45 độ
Xét ΔADM vuông tại A có góc ADM=45 độ
nên ΔADM vuông cân tại A
=>AD=AM
Bài 1:
a,
OM là đường trung bình của tam giác BAC => OM = 1/2*BC
OM = 1/2*AB
=> AB=BC (đpcm).
b,
Tam giác ABC đều => BC = 2*r(O)
MN là đường trung bình của tam giác ABC => MN = 1/2*AB = r(O) = OM = OB =BN => BOMN là hình thoi.
