Cho tam giác ABC có \(\widehat{A}\)=90 độ. Lấy điểm M thuộc đường thẳng BC. Vẽ MH\(\perp\)AB tại H và MK\(\perp\)AC tại K.Chứng minh \(\widehat{BMH}=\widehat{BCA,}\widehat{HBM}=\widehat{KMC}\)và tính \(\widehat{KMH}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:3 cạnh hình tam giác có tổng số đo bằng 180 độ
HBM +KMC=90 độ và HBM=KMC
KMH=90 độ
Mik đang học nên gợi ý tính KMH cho bạn và trả lời câu trên thôi
Chúc bạn học tốt!
ta có 3 cạnh tam giác bằng 180o
MBH+CMK=90o và MBH=CMK
HMK=90o


Vì mk vuông góc với ac và ab vuông góc với ac nên km song song ah.mh vuông góc với ah nên MHA=90 độ.Vì km song song với ah nên KMH+MHA=180 độ(2 goc trong cung phia)suy ra KMH +90 độ=180 độ.Suy ra KMH bằng 90 độ

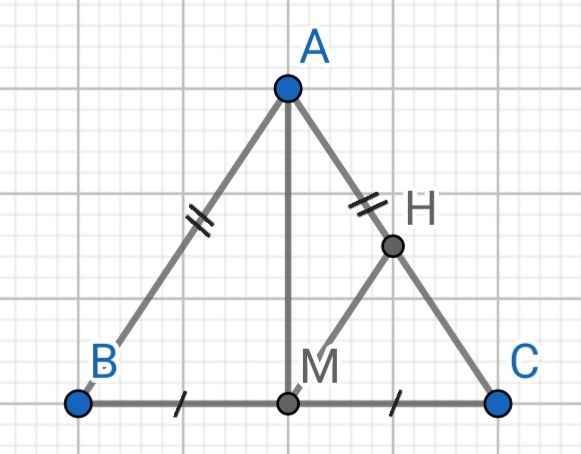 a) Xét ∆AMB và ∆AMC có:
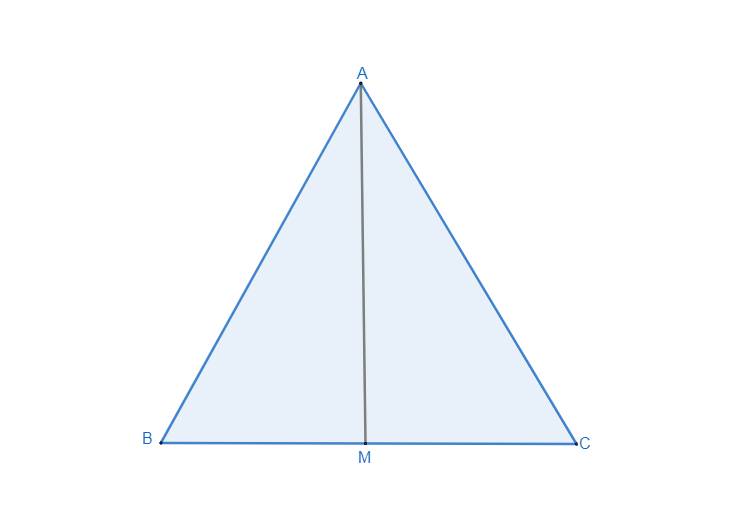
a) Xét ∆AMB và ∆AMC có:
AB = AC (gt)
AM là cạnh chung
MB = MC (do M là trung điểm của BC)
⇒ ∆AMB = ∆AMC (c-c-c)
b) Do ∆AMB = ∆AMC (cmt)
⇒ ∠AMB = ∠AMC (hai góc tương ứng)
Mà ∠AMB + ∠AMC = 180⁰ (kề bù)
⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰
⇒ AM ⊥ BC
c) Do ∆AMB = ∆AMC (cmt)
⇒ ∠ABM = ∠ACM (hai góc tương ứng)
⇒ ∠ABM = ∠HCM (1)
Do MH // AB (gt)
⇒ ∠ABM = ∠HMC (đồng vị) (2)
Từ (1) và (2) ⇒ ∠HMC = ∠HCM
Do ∆AMB = ∆AMC (cmt)
⇒ ∠MAB = ∠MAC (hai góc tương ứng)
⇒ ∠MAB = ∠HAM (3)
Do MH // AB (gt)
⇒ ∠MAB = ∠HMA (so le trong) (4)
Từ (3) và (4) ⇒ ∠HMA = ∠HAM

a: Xét tứ giác AEHD có
\(\widehat{AEH}=\widehat{ADH}=\widehat{DAE}=90^0\)
Do đó: AEHD là hình chữ nhật


Bn có thể cm bằng cách khác là chứng minh nó song song => nó bằng nhau vì đồng vị.
Này Băng Băng 2k6, bn có thể giải chứng minh \(\widehat{HBM}=\widehat{KMC}\)bằng cách chứng minh hai đường thẳng song song => nó bằng nhau vì đồng cị được ko chứ giải theo cách tam giác mk chưa đc hok