tính giá trị biểu thức sau:
C = ( tan210o / cot280o ) + ( tan220o : cot270o ) + ... + ( tan240o : cot250o ) + tan245o
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 12 2021
Đặt \(2000=a\)
\(A=a^9\\ B=\left(a-4\right)\left(a-3\right)\left(a-2\right)\left(a-1\right)a\left(a+1\right)\left(a+2\right)\left(a+3\right)\left(a+4\right)\\ B=\left(a^2-16\right)\left(a^2-9\right)\left(a^2-4\right)\left(a^2-1\right)a< a.a^2.a^2.a^2.a^2=a^9\\ B=\left(a-8\right)\left(a-6\right)\left(a-4\right)\left(a-2\right)a\left(a+2\right)\left(a+4\right)\left(a+6\right)\left(a+8\right)\\ C=\left(a^2-64\right)\left(a^2-36\right)\left(a^2-16\right)\left(a^2-4\right)a\\ C< \left(a^2-9\right)\left(a^2-4\right)\left(a^2-1\right)a< a.a^2.a^2.a^2=a^9\\ D=\left(a-20\right)\left(a-15\right)\left(a-10\right)\left(a-5\right)a\left(a+5\right)\left(a+10\right)\left(a+15\right)\left(a+20\right)\\ D=\left(a^2-400\right)\left(a^2-225\right)\left(a^2-100\right)\left(a^2-25\right)a\\ D< \left(a^2-64\right)\left(a^2-36\right)\left(a^2-16\right)\left(a^2-4\right)a< a.a^2.a^2.a^2=9\)
Vậy \(D< C< B< A\)
PT
1
PT
1
PT
1
CM
31 tháng 1 2019
Áp dụng tính chất cơ bản của phép cộng phân số để tính nhanh:
PT
1
S
29 tháng 11 2021
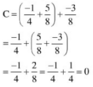
\(1.\) 12 x 11 + 21 x 11 x 11 + 11 x 33
= ( 12 x 11 ) + ( 21 x 11 x 11 ) + ( 11 x 33 )
= \(132+2541+363\)
= \(3036\)
132x11-11x32-54x11
= ( 132 x 11 ) - ( 11 x 32 ) - ( 54 x 11 )
\(=1452-352-594\)
= \(506\)
\(2.\)
45 x 32 + 1245
= ( 45 x 32 ) + 1245
= 1400 + 1245
= 2685
75 x 18 + 75 x 21
= ( 75 x 18 ) + ( 75 x 21 )
= 1350 + 1575
= 2925
12 x (27+46) -1567
= 12 x 73 - 1567
= ( 12 x 73 ) - 1567
= 876 - 1567
= - 691
PT
1
CM
17 tháng 10 2018
C = –1,7 . 2,3 + 1,7 . (–3,7) – 1,7 . 3 – 0,17 : 0,1.
= –1,7 . 2,3 – 1,7 . 3,7 – 1,7 . 3 – 0,17 .10
= –1,7 . 2,3 – 1,7 . 3,7 – 1,7 . 3 – 1,7.
= –1,7 . (2,3 + 3,7 + 3 + 1)
= –1,7 . 10 = –17.
CM
27 tháng 9 2019
a) x ≠ 2 và x ≠ 0
b) Rút gọn được Q = x + 1 2 x
c) Thay x = 2017 (TMĐK) vào Q ta được Q = 1009 2017
\(C=\frac{tan^210}{tan^2\left(90-80\right)}+\frac{tan^220}{tan^2\left(90-70\right)}+...+\frac{tan^240}{tan^2\left(90-50\right)}+tan^245\)
\(=\frac{tan^210}{tan^210}+\frac{tan^220}{tan^220}+\frac{tan^230}{tan^230}+\frac{tan^240}{tan^240}+1\)
\(=1+1+1+1+1=5\)