giải và biện luận các hệ phương trình
a) \(\sqrt{x^2-1}-x=m\)
b) \(\sqrt{x^2-4x+3}=\frac{1}{2}x-m\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 5 2015
a:dk: x>0;x khac 1; x khac 2
A=mở ngoăc vuông (2+căn x)^2-(2-căn x)^2+4x tất ca trên (4-x) đống ngăc vuông nhân voi (2căn x -x)/(căn x - x)
rút gon ngoăc vuông ta co (8căn x +4x)/(4-x) roi nhân vơi (2 căn x -x)/(căn x -3) rôi rút gon thu dươc 4x/(căn x -3)
b:4x/(Cx -3) > 0 * vi x >0 nen 4x > 0. vay muôn A>0 thi Cx-3 > 0 tương đương Cx>3 tương đương x>9
c; não quá tải. đợij lần sau
28 tháng 4 2021
(x2−2x+1+2)(2x−x2−1+7)=18(x2-2x+1+2)(2x-x2-1+7)=18
⇒[(x−1)2+2][7−(x−1)2]=18(1)⇒[(x-1)2+2][7-(x-1)2]=18(1)
Đặt (x−1)2=a(x-1)2=a
(1)⇔(a+2)(7−a)=18(1)⇔(a+2)(7-a)=18
⇒−a2+5a+14=18⇒-a2+5a+14=18
⇒a2−5a+4=0⇒a2-5a+4=0
Ta có a+b+c=1−5+4=0a+b+c=1-5+4=0
⇒a1=1⇒a1=1
a2=41=4a2=41=4
Thay (x−1)2=a(x-1)2=a vào ta được
[(x−1)2=1(x−1)2=4[(x−1)2=1(x−1)2=4
⇒⎡⎢ ⎢ ⎢⎣x−1=1x−1=−1x−1=2x−1=−2⇒[x−1=1x−1=−1x−1=2x−1=−2
⇒⎡⎢ ⎢ ⎢⎣x=2x=0x=3x=−1⇒[x=2x=0x=3x=−1
Vậy nghiệm của phương trình là x={−1;0;2;3}
31 tháng 5 2015
c}biến đổi thành \(x\left(m-1\right)=\left(m-1\right)\left(m+1\right)\)
với m=1 thì pt trở thành 0x=0 vậy pt đã cho có vô số nghiệm
với m\(\ne\)1 thì pt có nghiệm x=m+1
vậy ............
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 7 2021
\(y=\sqrt{\left(2x-1\right)^2}+\sqrt{\left(x-2\right)^2}=\left|2x-1\right|+\left|x-2\right|\)
\(y=\left[{}\begin{matrix}3x-3\left(\text{với }x\ge2\right)\\3-3x\left(\text{với }x\le\dfrac{1}{2}\right)\\x+1\left(\text{với }\dfrac{1}{2}\le x\le2\right)\end{matrix}\right.\)
Từ đó ta có đồ thị hàm số như sau:
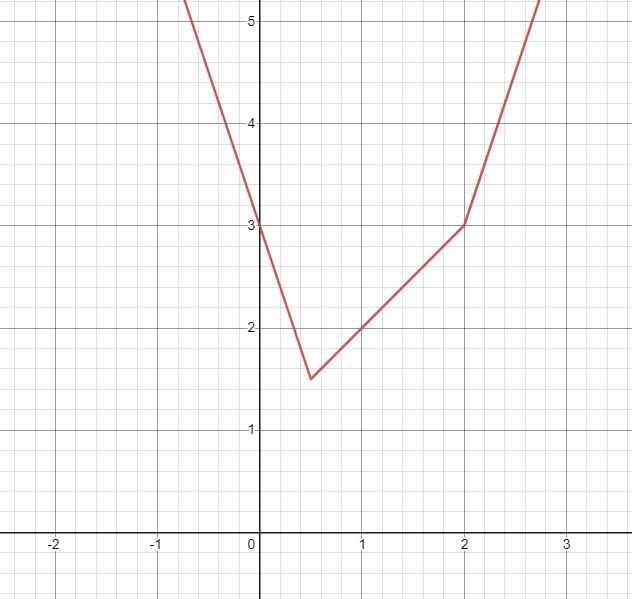
Từ đồ thị ta thấy phương trình \(\sqrt{4x^2-4x+1}+\sqrt{x^2-4x+4}=m\):
- Có đúng 1 nghiệm khi \(m=\dfrac{3}{2}\)
- Có 2 nghiệm phân biệt khi \(m>\dfrac{3}{2}\)
- Vô nghiệm khi \(m< \dfrac{3}{2}\)
*các phương trình