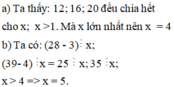Tìm dư \(x^{30}+x^4+x^{2015}+1\) cho \(x^{21}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để dọc cho dễ nhìn. Để chỉnh cho nha. ( Ko cs ý cướp công của bn)


Đặt x30 + x4 + x2015 + 1 = f(x) . Ta có : f(1) = 130 + 14 + 12015 + 1 = 4 ; f(-1) = (-1)30 + (-1)4 + (-1)2015 + 1 = 0.
Vì đa thức chia bậc 2 nên đa thức dư bậc 1 có dạng ax + b. Do đó :
f(x) = (x2 -1).q(x) + ax + b.
f(1) = (12 - 1).q(x) + a.1 + b = a + b ; f(-1) = ((-1)2 - 1).q(x) + a.(-1) + b = - a + b
Vậy a + b = 4 và - a + b = 0. Giải ra đc a = b = 2. Suy ra đa thức dư

đặt A=\(\left[\left(x+2\right)\left(x+8\right)\right]\left[\left(x+4\right)\left(x+6\right)\right]+2015\)
=\(\left(x^2+10x+16\right)\left(x^2+10x+24\right)+2015\)
=\(\left(x^2+10x+21-5\right)\left(x^2+10x+21+3\right)+2015\)
=\(\left(x^2+10x+21\right)^2-5\left(x^2+10x+21\right)+3\left(x^2+10x+21\right)-15+2015\)
=\(\left(x^2+10x+21\right)^2-2\left(x^2+10x+21\right)+2000\)
vì \(\left(x^2+10x+21\right)^2⋮x^2+10x+21\);\(-2\left(x^2+10x+21\right)⋮x^2+10x+21\)
SUY RA A\(:x^2+10x+21,\forall x\inℝ\)dư 2000
đáp số 2000
kb với mk nha!!!!




\(\left(x+2\right)\left(x+4\right)\left(x+6\right)\left(x+8\right)+2015\)
\(=\left[\left(x+2\right)\left(x+8\right)\right]\left[\left(x+4\right)\left(x+6\right)\right]+2015\)
\(=\left(x^2+10x+16\right)\left(x^2+10x+24\right)+2015\)
Đặt \(t=x^2+10x+21\) ta có \(\left(x^2+10x+16\right)\left(x^2+10x+24\right)+2015\)
\(=\left(t-5\right)\left(t+3\right)+2015\)
\(=t^2-2t+2010\)
=> Số dư khi chia đa thức đã cho cho đa thức x^2+10x+21 là 2010