Trong hình bên biết
\(\widehat{BAD}\)= 110o , \(\widehat{ABC}\)= 70o, \(\widehat{BCD}\)= 90O
Chứng minh hai đường thẳng a và d vuông góc với nhau.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

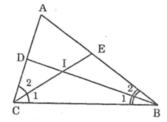
Ta có:
+ Trong ΔBIC có ∠BIC = 180º - (∠B1 + ∠C1) (1)
+ BI, CI là phân giác của ∠ABC và ∠BCA nên:
∠B1 = 1/2. ∠BAC; ∠C1 = 1/2. ∠ACB
⇒ ∠B1 + ∠C1 = 1/2. (∠BAC + ∠BCA) (2)
+ Trong ΔABC có: ∠BAC + ∠BCA = 180 - ∠A =140º (3).
Từ (1), (2) và (3) suy ra ∠BIC = 180º - 1/2.140º = 110º
Chọn đáp án C

Cho Â= 70o và B= 110o. Khẳng định nào sau đây là sai?
A. Â là góc nhọn. B. Â và \(\widehat{B}\) bù nhau. C. Góc B là góc tù.
D. Â và \(\widehat{B}\) kề bù (vì đề bài không cho góc B trùng góc A)
D nha. Vì người ta chx cho \(\widehat{A}\) và \(\widehat{B}\) cùng nằm trên 1 mặt phẳng!

a) Ta có: đường thẳng a là đường trung trực của đoạn thẳng AB và CD nên \(a \bot AB;a \bot CD\).
Suy ra: AB // CD.
b) Đường thẳng a là đường trung trực của đoạn thẳng AB và CD nên MN là đường trung trực của đoạn thẳng AB và CD. Suy ra: MD = MC.
Xét tam giác vuông MNC và tam giác vuông MND có: ND = NC; MD = MC.
Vậy \(\Delta MNC = \Delta MND\)(cạnh huyền – cạnh góc vuông).
c) \(\Delta MNC = \Delta MND\)nên \(\widehat {CMN} = \widehat {DMN}\).
Mà \(\widehat {AMN} = \widehat {BMN} = 90^\circ \Rightarrow \widehat {AMN} - \widehat {DMN} = \widehat {BMN} - \widehat {CMN}\).
Vậy \(\widehat {AMD} = \widehat {BMC}\).
d) Xét hai tam giác AMD và BMC có:
MA = MB;
\(\widehat {AMD} = \widehat {BMC}\);
MD = MC.
Vậy \(\Delta MAD = \Delta MBC\)(c.g.c). Suy ra: \(AD = BC,\widehat A = \widehat B\) (cặp cạnh và góc tương ứng).
e) \(\Delta MAD = \Delta MBC\) nên \(\widehat {ADM} = \widehat {BCM}\) (2 góc tương ứng).
\(\Delta MNC = \Delta MND\) nên \(\widehat {MCN} = \widehat {MDN}\) (2 góc tương ứng).
Vậy \(\widehat {ADM} + \widehat {MDN} = \widehat {BCM} + \widehat {MCN}\) hay \(\widehat {ADC} = \widehat {BCD}\).

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: Xét ΔCHM vuông tại H và ΔCKB vuông tại K có
góc HCM chung
=>ΔCHM đồng dạng với ΔCKB
=>CH/CK=CM/CB
=>CH*CB=CK*CM
giải
tự vẽ hình nha
a, xét △ ABC và △ HBA có
góc B chung
góc BHA = góc BAC = 90 độ
➜ △ABC ∼ △HBA (g.g)
b, xét △CHM và △CKB có
góc C chung
góc CHM = góc CKB
➜ △CHM ∼ △CKB (g.g)
c, xét △DHB và △CKB có
góc B chung
góc BKC = góc BHD = 90 độ
➜ △DHB∼△CKB (g.g)
vì △DHB∼△CKB
➜DH/CK = HB/KB = DB/CB
xét △BKH và △BCD có
góc B chung
HB/KB = DB/CB (CMT)
➜△BKH ∼ △BCD
vì △BKH ∼ △BCD nên góc BKH = góc BCD (hai góc tương ứng )