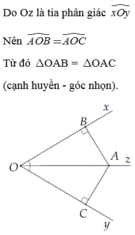
bài1. Cho góc nhọn xOy, Oz là tia phân giác. Lấy B thuộc Ox, C thuộc Oy, A thuộc Oz sao cho AB=AC và góc OCA, OBA là góc tù. C/m OB=OC
Bạn nào giúp mình với ạ!! Mình cần gấp!
C Cho gãc nhän xOy,Oz lμ ph©n gi ̧c.LÊy B
Ox, COy, AOz sao cho AB=AC vμ gãc
OCA,OBA lμ gãc tï,C/m: OB=OC ho gãc nhän xOy,Oz lμ ph©n gi ̧c.LÊy B
Ox, COy, AOz sao cho AB=AC vμ gãc OCA,OBA lμ gãc tï,C/m: OB=OC