Chứng minh định lí đường trung trực của đoạn thẳng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: Gọi O là điểm nằm trên đường trung trực của AB
=>OH⊥AB tại H
=>H là trung điểm của AB
Xét ΔOHA vuông tại H và ΔOHB vuông tại H có
OH chung
HA=HB
Do đó: ΔOHA=ΔOHB
Suy ra: OA=OB

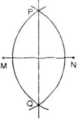
Ta có : Hai cung tròn tâm M và N có bán kính bằng nhau và cắt nhau tại P, Q.
Nên MP = NP và MQ = NQ
⇒ P; Q cách đều hai mút M, N của đoạn thẳng MN
nên theo định lí 2 : P; Q thuộc đường trung trực của MN
hay đường thẳng qua P, Q là đường trung trực của MN.
Vậy PQ là đường trung trực của MN.

Hướng dẫn:
Ta có: Hai cung tròn tâm M và N có bán kính bằng nhau
Nên MP = NP và MQ = NQ => P; Q cách đều hai mút M, N của đoạn thẳng MN nên P; Q thuộc đường trung trực của MN hay đường thẳng qua P, Q là đường trung trực của MN
Hướng dẫn:

Ta có: Hai cung tròn tâm M và N có bán kính bằng nhau
Nên MP = NP và MQ = NQ => P; Q cách đều hai mút M, N của đoạn thẳng MN nên P; Q thuộc đường trung trực của MN hay đường thẳng qua P, Q là đường trung trực của MN

x A O y M N
\(O\in Ox\)\(\Rightarrow OM=OA\)\(\left(1\right)\)(Ox là đường trung trực của MA)
\(O\in Oy\)\(\Rightarrow OA=OM\)\(\left(2\right)\)(Oy là dường trung trực AN)
Từ \(\left(1\right);\left(2\right)\Rightarrow OM=ON\)
Vì\(OM=ON\)\(\Rightarrow O\in\)đường trung trực của MN (O cách đều hai mút M và N)
Vậy đường trung trực của MN luôn đi qua 1 điểm là O.
b là sao bạn mk ko hiểu?

a: Ta có: M nằm trên đường trung trực của AB
nên MA=MB
b: Ta có: ΔMAB cân tại M
mà MI là đường trung trực
nên MI là đường phân giác

1. vd: đường thẳng d là đường trung trực của đoạn thẳng AB
- ta c/m đường thẳng d vuông góc vs đoạn thẳng AB tại trung điểm của AB
2. ta tìm giao của 2 đg thẳng sau đó c/m đg thẳng thứ 3 cx đi qua giao điểm đó
sử dụng các t/c đồng quy trong t.giác(sgk 7 tập 2)

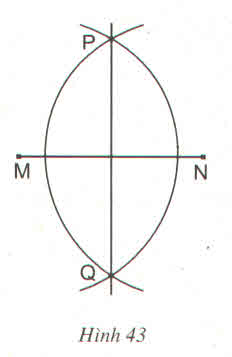
Ta có PM = PN ( bán kính đường tròn)
nên P ? đường trung trực của MN
QM = QN ( bán kính đường tròn)
? Q ? đường trung trực của MN
Vậy PQ là đường trung trực của đoạn
thẳng MN

Mọi điểm thuộc đường trung trực của 1 đoạn thẳng thì cách đều 2 đầu mút của đoạn thẳng đó
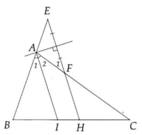
A B C H
CMR: Điểm A cách đều với điểm B và C
Bài làm
Xét tam giác AHB và tam giác AHC có:
\(\widehat{AHB}=\widehat{AHC}=90^0\)
Cạnh AH chung
BH = HC ( gt )
=> Tam giác AHB = tam giác AHC ( c.g.c )
=> AB = AC
=> Điểm A cách đều với điểm B và C ( đpcm )
# Học tốt #