a) (a2b2-5a)(a4b4+5a3b2+25a2)
b) (10a2-1)(100a4+10a2+1)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng AM-GM có:
\(2a^2+2b^2\ge4ab\)
\(8b^2+\dfrac{1}{2}c^2\ge4bc\)
\(8a^2+\dfrac{1}{2}c^2\ge4ac\)
Cộng vế với vế \(\Rightarrow VT\ge4\left(ab+bc+ac\right)=4\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}ab+bc+ac=1\\a=b=\dfrac{c}{4}\end{matrix}\right.\)\(\Rightarrow a=b=\dfrac{1}{3};c=\dfrac{4}{3}\)

Đáp án C
Phương pháp: Thêm bớt hạng tử để được các hằng đẳng thức.
Sử dụng kết quả A 2 + B 2 + C ≥ C để tìm min F và chú ý tìm điều kiện để dấu “=” xảy ra. 2
Cách giải: F = a 4 b 4 + b 4 a 4 − a 2 b 2 + b 2 a 2 + a b + b a
= a 2 b 2 − 1 2 + b 2 a 2 − 1 2 + a b + b a 2 + a b + b a − 4 ≥ a 2 + b 2 a b − 4 ≥ 2 − 4 = − 2
Dấu “=” xảy ra ⇔ a ; b = − 1 ; 1 hoặc a ; b = 1 ; − 1
Vậy M i n y = − 2 tại a ; b = − 1 ; 1 hoặc a ; b = 1 ; − 1

Câu 3:
#include <bits/stdc++.h>
using namespace std;
long long n;
int main()
{
cin>>n;
bool kt=true;
for (long long i=2; i<=sqrt(n); i++)
if (n%i==0)
{
kt=false;
break;
}
if ((kt==true) and (n>1)) cout<<"la so nguyen to";
else cout<<"khong la so nguyen to";
return 0;
}


Chọn A
+ Chia đều 10 đội vào 2 bảng A và B có ![]() cách.
cách.
Do đó số phần tử của không gian mẫu là : ![]()
+ Sắp xếp đội của lớp 10A1 và 10A2 vào 2 bảng khác nhau A và B có 2! cách.
Chọn 4 đội trong 8 đội còn lại để xếp vào bảng có đội lớp 10A1 có C 8 4 cách.
Bốn đội còn lại xếp vào bảng còn lại.
Suy ra số cách chia đều 10 đội vào 2 bảng sao cho 2 đội 10A1 và 10A2 nằm ở 2 bảng khác nhau là ![]()
Gọi A là biến cố “Chia đều 10 đội vào 2 bảng sao cho 2 đội 10A1 và 10A2 nằm ở 2 bảng khác nhau ” thì số các kết quả thuận lợi cho biến cố A là: ![]()
+ Xác suất cần tìm là: 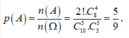

Đáp án A
Phương pháp: Sử dụng phương pháp tích phân từng phần tính F(x)
Cách giải:
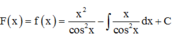
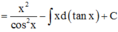
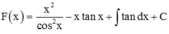
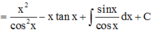

![]()
![]()
=> 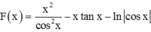
![]()
![]()
![]()
![]()
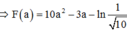
![]()
![]()