Giúp mình bài 8 với, cần gấp. Mình sẽ tặng Gp cho mỗi ai tl :
Cho tam giác abc, các điểm E,F thuộc đường pg AD sao cho ABE =DBF. Vẽ điểm I đối xứng E qua AB, H đối xứng E qua AC, K đối xứng F qua BC. Chứng minh ACE =DCF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 9 2019
a) Gọi F là giao diện của HI IH ta có :
I là giao điểu đối xứng của E qua AB,AC
Ta thấy I,H đối xứng với E qua AB,AC
=> Ta lại thấy các điểm EF thuộc đg phân giác AD ( Có cần vẽ ko bn?)
Mà đây là xác định 1 tam giác trực tuyến theo đường phân giác nên CMR để FH = FI ta có:
Để DM và góc ABE = DBF
Mà nếu FI để cùng thì sẽ FH tuy nhiên 2 cái ko bằng nhau (vô lý)
Để FI = FH là :
\(DEF=DBF=FH=IH\)
Vì vẽ qua đg đó nối liền vs nhau
b) K vẽ đối xứng BC nên mình k vẽ đc :)
K đi qua F -> từ F qua BC nên
Cmr:
FI=FK
cho thấy FI qua 1 đg đối xứng nhất địng
c) Bí...
16 tháng 10 2021
a: Ta có: E và H đối xứng nhau qua AB
nên AB là đường trung trực của EH
Suy ra: AB\(\perp\)EH tại M và M là trung điểm của EH
Ta có: H và F đối xứng nhau qua AC
nên AC là đường trung trực của HF
Suy ra: AC\(\perp\)HF tại N và N là trung điểm của FH
Xét tứ giác AMHN có
\(\widehat{MAN}=\widehat{ANH}=\widehat{AMH}=90^0\)
Do đó: AMHN là hình chữ nhật
CM
17 tháng 12 2019
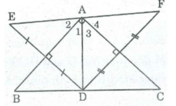
* Vì E đối xứng với D qua AB
⇒ AB là đường trung trực của đoạn thẳng DE
⇒ AD = AE (tính chất đường trung trực)
Nên ∆ ADE cân tại A
Suy ra: AB là đường phân giác của ∠ (DAE) ⇒ ∠ A 1 = ∠ A 2
* Vì F đối xứng với D qua AC
⇒ AC là đường trung trực của đoạn thẳng DF
⇒ AD = AF (tính chất đường trung trực)
Nên ∆ ADF cân tại A
Suy ra: AC là phân giác của ∠ (DAF)
⇒ ∠ A 3 = ∠ A 4
∠ (EAF) = ∠ EAD) + ∠ (DAF) = ∠ A 1 + ∠ A 2 + ∠ A 3 + ∠ A 4 = 2( ∠ A 1 + ∠ A 3 ) = 2 . 90 0 = 180 0
⇒ E, A, F thẳng hàng có AE = AF = AD
Nên A là trung điểm của EF hay điểm E đối xứng với điểm F qua điểm A.
5 tháng 7 2021
* Vì E đối xứng với D qua AB
⇒ AB là đường trung trực của đoạn thẳng DE
⇒ AD = AE (tính chất đường trung trực)
Nên ∆ ADE cân tại A
Suy ra: AB là đường phân giác của ∠ (DAE) ⇒ ∠ A 1 = ∠ A 2
* Vì F đối xứng với D qua AC
⇒ AC là đường trung trực của đoạn thẳng DF
⇒ AD = AF (tính chất đường trung trực)
Nên ∆ ADF cân tại A
Suy ra: AC là phân giác của ∠ (DAF)
ok!!!!
up lên nào, bài này khá khó :D