Cho tam giác ABC, Chứng minh rằng
- Nếu đường thẳng m song song vs cạnh BC thì m sẽ cắt các đường thẳng AB, AC.
- Nếu đường thẳng m song song vs cạnh BC và cắt cạnh AB thì m sẽ cắt cạnh AC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Giả sử m không cắt AB, AC. Thật vậy ta suy ra m // AB và m // AC. Suy ra AB // AC // BC (mâu thuẫn với giả thiết ABC là tam giác). Vậy ta có đpcm.
b) Giả sử m không cắt AC. Thật vậy ta suy ra m // AC. Suy ra AC // BC (mâu thuẫn với giả thiết ABC là tam giác). Vậy ta có đpcm.

a: m//BC
BC cắt AB tại B
Do đó: m cắt AB
m//BC
BC cắt AC tại C
Do đó: m cắt AC
b: m//BC
BC cắt AC
Do đó: m cắt AC

a: Vì m song song với BC
và AB cắt BC tại B
nên m cắt AB
Vì m//BC
và AC cắt BC tại C
nên m cắt AC
b: Vì m//BC
và BC cắt AC
nên m cắt AC

Chứng minh được ADME là hình bình hành Þ I là trung điểm của AM. Tương tự 2A. I thuộc đường trung bình của D ABC (đường thẳng đi qua trung điểm của AB và AC)
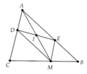

zì \(\hept{\begin{cases}MD//AE\\ME//AD\end{cases}}\)
=> tứ giác ADME là hbh
=>\(\hept{\begin{cases}AD=ME\\AE=MD\end{cases}}\)
=>\(\frac{AD}{AB}=\frac{ME}{AB}\)
mà ME//AB
=>\(\frac{ME}{AB}=\frac{CE}{AC}=>\frac{AD}{AB}=\frac{CE}{AC}\)
=>\(\frac{AD}{AB}+\frac{AE}{AC}=\frac{CE}{AC}+\frac{AE}{AC}=\frac{CE+AE}{AC}=\frac{AC}{AC}=1\left(dpcm\right)\)

không chứng minh được đâu bạn ạ. Nếu đường thẳng m song song với BC thì nó cũng có thể nằm ngoài tam giác ABC.
Ta cần phải có thêm điều kiện mới giải được bài toán.
=> Đầu bài thiếu dữ kiện

a: ME//AB
=>góc CEM=góc CAB=60 độ
=>góc CEM=góc C
Xét tứ giác MECD có
MD//EC
góc MEC=góc DCE
=>MECD là hình thang cân
=>góc EMD=180-60=120 độ
MF//BC
=>góc AFM=góc ABC=60 độ
Xét tứ giác AFME có
ME//AF
góc MFA=góc EAF
=>AFME là hình thang cân
=>góc FME=180-60=120 độ
MD//AC
=>góc MDB=góc ACB=60 độ
=>góc MDB=góc B
Xét tứ giác BFMD có
FM//BD
góc B=góc MDB
=>BFMD là hình thang cân
=>góc FMD=180-60=120 độ
=>góc FME=góc FMD=góc DME
b: AEMF là hình thang cân
=>AM=EF
BFMD là hình thang cân
=>BM=FD
MECD là hình thang cân
=>MC=ED
=>MA,MB,MC lần lượt là độ dài 3 cạnh của ΔDEF
=>Trong 3 đoạn MA,MB,MC, đoạn lớn nhất nhỏ hơn tổng 2 đoạn còn lại
Hình bạn tự vẽ!
a) Giả sử m không cắt \(AB,AC\). Thật vậy
=> \(m\) // \(AB\) và \(m\) // \(BC.\)
=> \(AB\) // \(AC\) // \(BC\) (vô lí với gt \(\Delta ABC\))
=> \(m\) sẽ cắt các đường thẳng \(AB,AC.\)
Vậy ta có đpcm.
b) Gỉa sử m không cắt \(AC.\) Thậy vậy
=> \(m\) // \(AC\)
=> \(AC\) // \(BC\) (vô lí với gt \(\Delta ABC\))
=> \(m\) sẽ cắt cạnh \(AC.\)
Vậy ta có đpcm.
Chúc bạn học tốt!
Thanks