Tính diện tích hình bình hành có hai cạnh 12cm và 15cm, góc tạo bởi hai cạnh ấy bằng 110 độ.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giả sử hình bình hành MNPQ có MN = 12cm, MQ = 15cm, ∠ NMQ = 1100
Ta có: ∠ NMQ + ∠ MNP = 180 ° (hai góc trong cùng phía)
Suy ra: ∠ MNP = 180 ° - ∠ NMQ
= 180 ° - 110 ° = 70 °
Kẻ MR ⊥ NP
Trong tam giác vuông MNR, ta có:
MR = MN.sin ∠ MNP =12.sin 70 ° ≈ 11,276 (cm)
Vậy S M N P Q = MN.NP ≈ 11,276.15 = 169,14 ( c m 2 )

giả sử góc a=135 độ , thì góc d=45 độ.kẻ đường cao ah khi đó góc dah=45 độ vậy tam giác adh cân và vuông.áp dụng pytago ah=6.căn bậc hai của 2.vậy diện tích hbh=15.6 căn bậc 2 của 2=90.căn bậc 2 của 2(cm^2)
vì ABCD là hình bình hành
=> AD // BC ( tính chất )
=> \(\widehat{A}+\widehat{B}=180^0\)( hai góc trong cùng phía)
=> \(\widehat{B}=180^0-110^0=70^0\)
Kẻ AH\(\perp\)BC tại H, ta có tam giác vuông ABH
Xét tam giác vuông ABH, có:
AH=AB*sin B=12*sin 70 độ
\(AH\approx11,276\)(cm)
ta có: AD=BC ( ABCD là hình chữ nhật )
\(\Rightarrow S_{ABCD}=AH\cdot BC\approx11,276\cdot15=169,14\)(\(cm^2\))

Giả sử ta có hình bình hành ABCD, đường chéo AC, AB=12cm, AC=10cm, `\hat(ABC)=150^o`.
`S_(ABC) = 1/2 . 10. 12 . sinABC = 30 (cm^2)`
Vì đường chéo AC chia hình bình hành ABCD ra 2 tam giác bằng nhau.
`=> S_(ABCD) = 2.S_(ABC) = 60(cm^2)`
`=>` B.

A B C D H
Gọi hình bình hành đó là ABCD , từ A kẻ đường cao AH xuống cạnh CD (H thuộc CD)
Ta có : \(AH=AD.sinD\)
\(\Rightarrow S_{ABCD}=CD.AH=CD.AD.sinD\)
Vậy ta có điều phải chứng minh

A) Vẽ t/g ABC (A là góc nhọn), đường cao BH.
1/2.AB.AC.sinA = 1/2.AB.AC.(BH/AB) = 1/2.BH.AC = S(ABC)
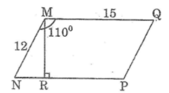
110 12 15 M N R P Q
Giả sử hình bình hành \(MNPQ\) có \(MN=12cm,MQ=15cm,\widehat{MNQ}=110^o\)
Ta có \(\widehat{NMQ}+\widehat{MNP}=180^o\) ( hai góc trong cùng phía )
mà \(\widehat{NMQ}=110^o\)
\(\Rightarrow\widehat{MNP}=180^o-110^o=70^o\)
Kẻ \(MR\perp NP\)
Trong tam giác vuông \(MNR\) ta có :
\(MR=MN.sin\widehat{MNP}\)
\(=12.sin70^o\approx11,276\)
Vậy \(S_{MNPQ}=MR.MQ\approx11,276.15=169,14\left(cm^2\right)\)
Chúc bạn học tốt !!!