chào mọi người mình là thành viên mới và hiện đang gặp khó khăn trong một bài toán này mon mọi người giúp đỡ ạ :
BT : cho 3 tập hợp E,F,G
chứng minh
E giao (FVG) = ( E giao F )* V( E giao G)
-------------------------------------------------------------------------------------------------------------------------------------------------------
mik không hiểu bài toán nên không làm được bước nào mong mọi người thông cảm .
FVG nghĩa là F nhân V nhân G
* nghĩa là nhân

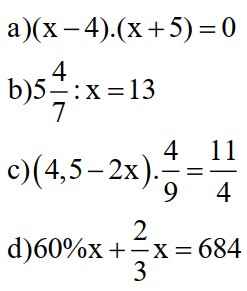 mọi người giúp e với hnay e gặp quá nhiều bài khó nên rất nguy mong mọi người giúp đỡ ạ
mọi người giúp e với hnay e gặp quá nhiều bài khó nên rất nguy mong mọi người giúp đỡ ạ