Cho biết sinα = \(\frac{4}{5}\) . Tính cosα ; tanα ; cotα
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TT
Trần Thị Như Ý
26 tháng 8 2019
https://i.imgur.com/DS9QNEp.jpg
Đúng(0)
Những câu hỏi liên quan
CM
28 tháng 9 2018
a, Tìm được sinα = 24 5 , tanα = 24 , cotα = 1 24
b, cosα = 5 3 , tanα = 2 5 , cotα = 5 2
c, sinα = ± 2 5 , cosα = ± 1 5 , cotα = 1 2
d, sinα = ± 1 10 , cosα = ± 3 10 , tanα = 1 3
23 tháng 8 2021
Bài 1:
\(\cos\alpha=\sqrt{1-\dfrac{9}{25}}=\dfrac{4}{5}\)
\(\tan\alpha=\dfrac{3}{5}:\dfrac{4}{5}=\dfrac{3}{4}\)
Bài 2:
\(\sin\alpha=\sqrt{1-\dfrac{49}{100}}=\dfrac{\sqrt{51}}{10}\)
\(\tan\alpha=\dfrac{\sqrt{51}}{7}\)
CM
9 tháng 3 2018
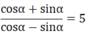
⇔ cosα + sinα = 5(cosα - sinα)
⇔ cosα + sinα = 5cosα - 5sinα
⇔ 6sinα = 4cosα
21 tháng 10 2021
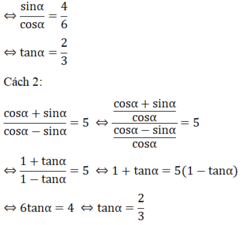
a: \(\cos\alpha=\dfrac{1}{2}\)
\(\tan\alpha=\sqrt{3}\)
\(\cot\alpha=\dfrac{\sqrt{3}}{3}\)
ND
1
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 10 2021
\(A=\dfrac{\dfrac{sina}{cosa}+\dfrac{cosa}{cosa}}{\dfrac{sina}{cosa}-\dfrac{cosa}{cosa}}=\dfrac{tana+1}{tana-1}=\dfrac{\sqrt{3}+1}{\sqrt{3}-1}=2+\sqrt{3}\)
TS
1
6 tháng 7 2023
3/4pi<a<pi
=>sin a>0; cosa<0
sin2a=-4/5
=>2*sina*cosa=-4/5
=>sina*cosa=-2/5
(sina-cosa)^2=sin^2a+cos^2a-2*sina*cosa=1+4/5=9/5
=>sin a-cosa=3/căn 5
CM
10 tháng 8 2019
Ta có sin α + cos α = a ⇒ sin α + cos α 2 = a 2
⇔ sin 2 α + 2 sin α cos α + c os 2 α = a 2 ⇔ 1 + 2 sin α cos α = a 2 ⇔ sin α cos α = a 2 − 1 2 .
Chọn C.
H9
HT.Phong (9A5)
CTVHS
24 tháng 8 2023
Ta có:
\(cot\alpha\cdot tan\alpha=1\)
\(\Rightarrow cot\alpha=\dfrac{1}{tan\alpha}\)
\(\Rightarrow cota=\dfrac{1}{\dfrac{3}{4}}=\dfrac{4}{3}\)
Mà:
\(cot^2\alpha+1=\dfrac{1}{sin^2\alpha}\)
\(\Rightarrow sin\alpha=\sqrt{\dfrac{1}{cot^2\alpha+1}}\)
\(\Rightarrow sin\alpha=\sqrt{\dfrac{1}{\left(\dfrac{4}{3}\right)^2+1}}=\dfrac{3}{5}\)
Lại có:
\(cos^2\alpha+sin^2\alpha=1\)
\(\Rightarrow cos\alpha=\sqrt{1-sin^2a}\)
\(\Rightarrow cos\alpha=\sqrt{1-\left(\dfrac{3}{5}\right)^2}=\dfrac{4}{5}\)
GH
24 tháng 8 2023
\(tan\alpha=\dfrac{3}{4}\\ \Rightarrow cot\alpha=1:\dfrac{3}{4}=\dfrac{4}{3}\)
Có:
\(1+cot^2\alpha=\dfrac{1}{sin^2\alpha}\\ \Rightarrow sin\alpha=\sqrt{1:\left(1+\left(\dfrac{4}{3}\right)^2\right)}=\dfrac{3}{5}\)
\(\Rightarrow cos\alpha=\sqrt{1-\left(\dfrac{3}{5}\right)^2}=\dfrac{4}{5}\)