Tìm min \(A=x^4+7x^2-4x+2038\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CC
0
CC
1
ML
4 tháng 7 2015
\(\text{Tử }=\left(x^2-8x+16\right)+\left(x-2-2\sqrt{x-2}.\sqrt{2}+2\right)+2022\)
\(=\left(x-4\right)^2+\left(\sqrt{x-2}-\sqrt{2}\right)^2+2022\ge2022\)
Dấu "=" xảy ra khi \(x-4=0\text{ và }\sqrt{x-2}=\sqrt{2}\Leftrightarrow x=4\).
\(\text{Mẫu }=\sqrt{x-3}+\sqrt{5-x}\)
Ta có: \(\left(a-b\right)^2\ge0\Rightarrow a^2+b^2-2ab\ge0\Rightarrow2\left(a^2+b^2\right)\ge a^2+b^2+2ab=\left(a+b\right)^2\)
Dấu "=" xảy ra khi a = b.
\(\Rightarrow\left(\sqrt{x-3}+\sqrt{5-x}\right)^2\le2\left(x-3+5-x\right)=4\)
\(\Rightarrow\sqrt{x-3}+\sqrt{5-x}\le2\)
Dấu "=" xả ra khi \(\sqrt{x-3}=\sqrt{5-x}\Leftrightarrow x=4\)
\(\Rightarrow Q\ge\frac{2022}{2}=1011\)
Dấu "=" xảy ra khi x = 4.
Vậy GTNN của Q là 1011 khi x = 4.
DT
0
HT
1
23 tháng 12 2023
\(B=3x^2+3x-1\)
\(=3\left(x^2+x-\dfrac{1}{3}\right)\)
\(=3\left(x^2+x+\dfrac{1}{4}-\dfrac{7}{12}\right)\)
\(=3\left(x+\dfrac{1}{2}\right)^2-\dfrac{7}{4}>=-\dfrac{7}{4}\forall x\)
Dấu '=' xảy ra khi x+1/2=0
=>\(x=-\dfrac{1}{2}\)
\(C=-2x^2+7x+3\)
\(=-2\left(x^2-\dfrac{7}{2}x-\dfrac{3}{2}\right)\)
\(=-2\left(x^2-2\cdot x\cdot\dfrac{7}{4}+\dfrac{49}{16}-\dfrac{73}{16}\right)\)
\(=-2\left(x-\dfrac{7}{4}\right)^2+\dfrac{73}{8}< =\dfrac{73}{8}\forall x\)
Dấu '=' xảy ra khi x-7/4=0
=>x=7/4
DT
6
KN
29 tháng 7 2019
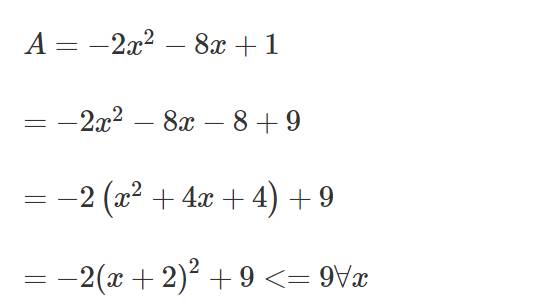
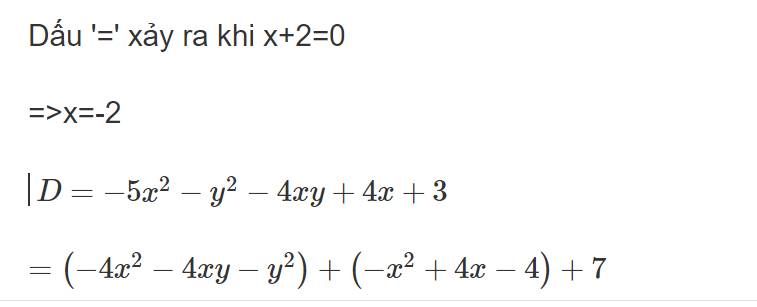
\(A=x^2-6x-4=x^2-6x+9-13=\left(x-3\right)^2-13\ge-13\)
Vậy \(A_{min}=-13\Leftrightarrow x=3\)
KN
29 tháng 7 2019
\(B=x^2-x+1=x^2-2.\frac{1}{2}x+\frac{1}{4}+\frac{3}{4}=\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}\)
Vậy \(B_{min}=\frac{3}{4}\Leftrightarrow x=\frac{1}{2}\)
min a nếu x = 0
=>0 + 0 - 0 + 2038
=> A = 2038
Hội con 🐄 chúc bạn học tốt!!!
\(A=x^4+6x^2+3^2+x^2-4x+2^2+2025.\)
\(A=\left(x^2+3\right)^2+\left(x-2\right)^2+2025\)
Vì \(\hept{\begin{cases}\left(x^2+3\right)^2\ge0\forall x\\\left(x-2\right)^2\ge0\forall x\end{cases}}\Rightarrow\left(x^2+3\right)^2+\left(x-2\right)^2+2025\ge2025\forall x\)
Dấu '' = " xảy ra khi
\(\left(x^2+3\right)^2=0\) hoặc \(\left(x-2\right)^2=0\)
\(\Rightarrow x=\pm\sqrt{3}\) \(\Rightarrow x=2\)
Vậy \(Min_A=2025\Leftrightarrow x=\pm\sqrt{3};x=2\)
Study well