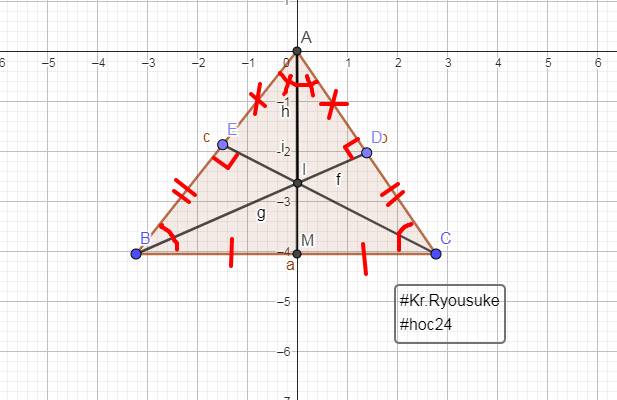
Cho tam giác ABC cân tại A. Hai đường phân giác BD, CE cắt nhau tại O (D thuộc AC, E thuộc AB).
a)C/m BE=CD
b) C/m tamgiacs cân
c) Tứ giác CDBE là hình gì?
d) Gọi M là trung điểm BC. C/m A,O,M thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 5 2023
a: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
góc EBC=góc DCB
=>ΔEBC=ΔDCB
=>BE=DC
=>AE=AD
b: Xét ΔAEI vuông tại E và ΔADI vuông tại D có
AI chung
AE=AD
=>ΔAEI=ΔADI
=>góc EAI=góc DAI
=>AI là phân giác của góc BAC
c: ΔABC cân tại A
mà AM là trung tuyến
nên AM là phân giác của góc BAC
=>A,I,M thẳng hàng
15 tháng 5 2023
`a,`
Vì `\Delta ABC` cân tại A
`-> \text {AB = AC, }` $\widehat {B} = \widehat {C}$
Xét `2\Delta` vuông và `BEC` và `CDB`:
`\text {BC chung}`
$\widehat {B} = \widehat {C}$
`=> \Delta BEC = \Delta CDB (ch-gn)`
`-> \text {BE = CD (2 cạnh tương ứng)}`
`b,`
Ta có: \(\left\{{}\begin{matrix}\text{AB = AE + BE}\\\text{AC = AD + CD}\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}\text{AB = AC}\\\text{BE = CD}\end{matrix}\right.\)
`-> \text {AE = AD}`
Xét `2\Delta` vuông `AEI` và ` ADI`:
`\text {AE = AD}`
`\text {AI chung}`
`=> \Delta AEI = \Delta ADI (ch-cgv)`
`->` $\widehat {EAI} = \widehat {DAI} (\text {2 góc tương ứng})$
`-> \text {AI là tia phân giác của}` $\widehat {EAD}$
Mà \(\text{E}\in\text{AB, D}\in\text{AC}\)
`-> \text {AI là tia phân giác của}` $\widehat {BAC}$ `(1)`
`c,`
Vì M là trung điểm của AC
`-> \text {AM là đường trung tuyến của} \Delta ABC` `(2)`
Từ `(1)` và `(2)`
`-> \text {Ba điểm A, I, M thẳng hàng.}`
TT
19 tháng 1 2021
A) Ta có tam giác ABC cân
=> AB = AC
Mà AD + DB = AB
AE + EC = AC
=> DB = EC ( AD = AE gt)
b) đề phải là BE và CD cắt nhau tại I
Ta có AD = AE
=> Tam giác ADE cân tại A
=> Góc ADE = Góc AED
=> Góc EDB = Góc DEC ( Cùng cộng nhau bằng 180 độ )
Xét Tam giác DEB và tám giác EDC có
BD = EC (cmt)
Góc EDB = Góc DEC (cmt)
DE là cạnh chung
=> Tam giác DEB và tam giác EDC (c-g-c)
=> Góc DBE = Góc ECD
=> Góc IBC = Góc ICB ( cùng cộng góc DBE và Góc ECD bằng hai góc ABC và Góc ACB)
=> Tam giác IBC cân
c) Ta có tam giác ADE cân \(\Leftrightarrow\widehat{ADE}=\frac{180^o-\widehat{A}}{2}\left(1\right)\)
Và tam giác ABC cân \(\Leftrightarrow\widehat{ABC}=\frac{180^o-\widehat{A}}{2}\left(2\right)\)
Từ (1) và (2)\(\Leftrightarrow\widehat{ADE}=\widehat{ABC}\)
Hai góc này ở vị trí đồng vị bằng nhau
=> DE // BC (đpcm)
d) Ta có điểm I cách đều cạnh AB và AC
=> AI là tia phân giác của tam giác ABC
trong tam giác cân tia phân giác cũng là đường cao
=> AI vuông góc với BC
E) chứng minh HI là tia phân giác của tam giác BHC
thì ba điểm thẳng hàng
a) Xét tam giác BEC và tam giác CDB
+) BC Chung
+) \(\widehat{EBC}=\widehat{DCB}\)
+) \(\widehat{BCE}=\widehat{DBC}=\frac{1}{2}\left(\widehat{ABC}\right)=\frac{1}{2}\widehat{ACB}\)
Vậy tam giác BEC = tam giác CDB ( g.c.g)
Suy ra BE = CD (2 cạnh tương ứng)
b) ?
c) Xét tam giác ABC.Theo định lý Ta-lét đảo:
\(\hept{\begin{cases}AB=AC\\EB=CD\end{cases}\Rightarrow}\frac{BE}{BA}=\frac{CD}{CA}\)
Vậy ED//BC(1)
\(\widehat{ABC}=\widehat{ACB}\left(2\right)\)
Từ (1)(2) ta có CDBE là hình thang cân
d) O là giao của 2 tia phân giác BD và CE
Vậy AO là phân giác của góc BAC
Ta có ABC là tam giác cân nên AM vừa là trung tuyến vừa là phân giác
Suy ra góc A chỉ có 1 tia phân giác hay A,O,M thẳng hàng