Giúp mk nha
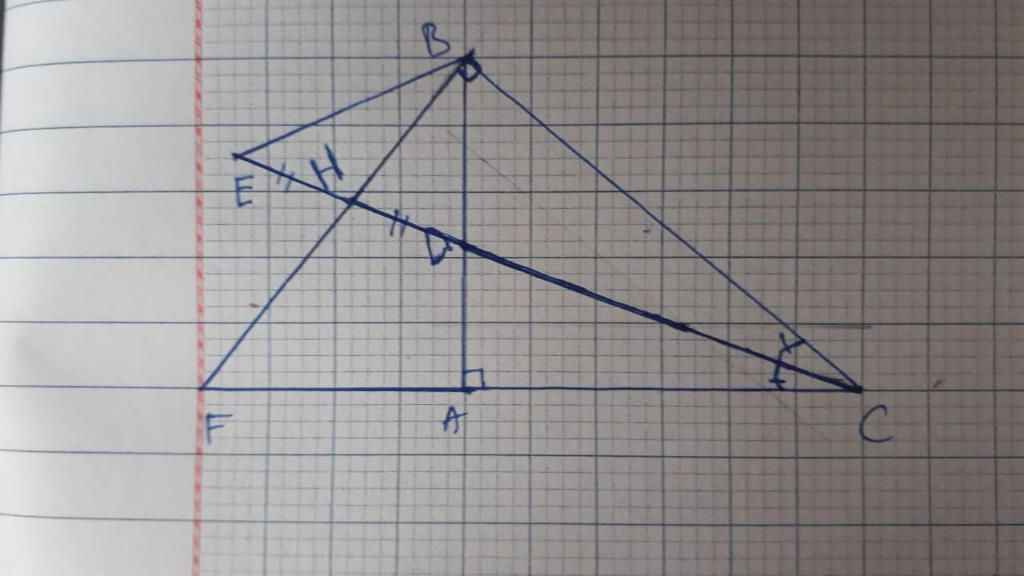
Cho tam giác ABC vuông tại A,phân giác CD
H là hình chiếu của B lên đừng thẳng CD
Trên CD lấy điểm Esao cho H là trung điểm của DE
F là giao điểm của BH và CA
Cm:a, góc CBE=góc ADC
b, BE vuông góc BC
c, DF song song BE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 7 2021
a,△BED có H là trung điểm của DE và BH ┴ DE
=> △BED cân ở B
=> ∠BED = ∠BDE
∠BDE = ∠ADC (đối đỉnh)
=> ∠BED = ∠ADC
△BED cân ở B => BH là phân giác của ∠EBD
=> ∠EHB = ∠DBH
mà ∠DBH = 90⁰ - ∠BFA = 90⁰ - ∠HFC = ∠ACD
=> ∠EBH = ∠ACD
b, ∠EBH = ∠ACD = ∠DCB (vì CH là phân giác của ∠ACB)
= 90⁰ - ∠CBH
=> ∠EHB + ∠CBH = 90⁰
=> BE ┴ BC
c, △FBC có CH ┴ BF ; BA ┴ FC ; CH ⋂ BA = {D}
=> D là trực tâm của △FBC
=> FD ┴ BC
BE ┴ BC
=> FD//BE
SN
31 tháng 7 2015
a,△BED có H là trung điểm của DE và BH ┴ DE
=> △BED cân ở B
=> ∠BED = ∠BDE
∠BDE = ∠ADC (đối đỉnh)
=> ∠BED = ∠ADC
△BED cân ở B => BH là phân giác của ∠EBD
=> ∠EHB = ∠DBH
mà ∠DBH = 90⁰ - ∠BFA = 90⁰ - ∠HFC = ∠ACD
=> ∠EBH = ∠ACD
b, ∠EBH = ∠ACD = ∠DCB (vì CH là phân giác của ∠ACB)
= 90⁰ - ∠CBH
=> ∠EHB + ∠CBH = 90⁰
=> BE ┴ BC
c, △FBC có CH ┴ BF ; BA ┴ FC ; CH ⋂ BA = {D}
=> D là trực tâm của △FBC
=> FD ┴ BC
BE ┴ BC
=> FD//BE
HT
24 tháng 5 2016
a,\(\Delta\)BED có H là trung điểm của DE và BH \(\perp\) DE
=> \(\Delta\)BED cân ở B
=> Góc BED = Góc BDE
Góc BDE = Góc ADC (đối đỉnh)
=> Góc BED = Góc ADC
\(\Delta\)BED cân ở B => BH là phân giác của góc EBD
=> gócEHB = gócDBH
mà gócDBH = 90⁰ - gócBFA = 90⁰ - gócHFC = gócACD
=> gócEBH = gócACD
b, gócEBH = gócACD = gócDCB (vì CH là phân giác của gócACB)
= 90⁰ - gócCBH
=> gócEHB + gócCBH = 90⁰
=> BE \(\perp\) BC
c, △FBC có CH \(\perp\) BF ; BA \(\perp\) FC ; CH \(\cap\) BA = D
=> D là trực tâm của \(\Delta\)FBC
=> FD \(\perp\) BC
BE \(\perp\) BC
=> FD//BE
MK
18 tháng 7 2017
1) a,△BED có H là trung điểm của DE và BH ┴ DE
=> △BED cân ở B
=> ∠BED = ∠BDE
∠BDE = ∠ADC (đối đỉnh)
=> ∠BED = ∠ADC
△BED cân ở B => BH là phân giác của ∠EBD
=> ∠EHB = ∠DBH
mà ∠DBH = 90⁰ - ∠BFA = 90⁰ - ∠HFC = ∠ACD
=> ∠EBH = ∠ACD
b, ∠EBH = ∠ACD = ∠DCB (vì CH là phân giác của ∠ACB)
= 90⁰ - ∠CBH
=> ∠EHB + ∠CBH = 90⁰
=> BE ┴ BC
c, △FBC có CH ┴ BF ; BA ┴ FC ; CH ⋂ BA = {D}
=> D là trực tâm của △FBC
=> FD ┴ BC
BE ┴ BC
=> FD//BE
DT
21 tháng 4 2019
a, Xét 2 t.giác vuông BHE và BHD có:
HD=HE(gt)
HB cạnh chung
=> t.giác BHE=t.giác BHD(cạnh góc vuông- cạnh góc vuong)
=> \(\widehat{EBH}\)=\(\widehat{DBH}\)(2 góc tương ứng)
=> BH là p/g của \(\widehat{EBD}\)<=>BF là p/g của \(\widehat{EBD}\)
Mik nghĩ phần a) sai đề. Phần a) phải chứng minh góc CBH= góc ADC
a) Có: CD là tia phân giác của góc C
=> góc ACD= góc BCH
Mà góc BCH+góc CBH=90o
góc ACD+góc ADC=90o
=> góc CBH=góc ADC (đpcm)
b) Dễ c/m: tam giac BHE=tam giac BHD (c.g.c)
=> góc BEH=góc BDH (t/ư)
=> góc BEC=góc CBH (=góc CDA)
Mà góc CBH+góc BCH=90o
=> góc BEC+góc BCH=90o
=> góc CBE=90o
=> BE vuông góc với BC
c) Dễ c/m: tam giác CBH=tam giác CFH (g.c.g)
=> CF=CB (t/ư)
=> tam giác CDF=tam giác CDB (c.g.c)
=> DF=DB (t/ư)
=> tam giác DBF cân tại D
=> góc DBF=góc DFB
Mà góc DBF=góc EBF
=> góc EBF=góc DFB
Mà 2 góc này ở vị trí so le trong
=> DF song song với BE
NHỚ TÍCH CHO MIK NHÉ ^^