Vẽ hình bình hành có độ dài một cạnh bằng 6 cm, một cạnh bằng 3 cm.Nêu các bước làm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
1
TM
2
VT
11 tháng 10 2021
-Vẽ đoạn thẳng AB=6cm và đoạn thẳng AD=4cm vuông góc với nhau.
-Qua B vẽ đường thẳng vuông góc với AB.
-Qua D vẽ đường thẳng vuông góc với AD.Hai đường thẳng này cắt nhau ở C.
=> ABCD là hình chữ nhật cần vẽ
11 tháng 10 2021
Ve chieu dai AB dai 6cm. ve canh BC dai 4cm. ke CD song song va bang AB .
O
3 tháng 5 2022
Chiều cao HBH là :
\(120\times\dfrac{5}{6}=100\left(cm\right)\)
Diện tích HBH là :
\(120\times100=12000\left(cm^2\right)\)
Đ/s :...
3 tháng 5 2022
Chiều cao hình bình hành
120 x \(\dfrac{5}{6}\)= 100 (cm)
Diện tích hình bình hành
120 x 100= 12000 (cm2)
19 tháng 10 2021
TL:
a) Diện tích hình vuông là:
5 x 5 = 25 ( cm2 )
Đ/S: 25cm2
7 tháng 5 2016
chiều cao là:
120x\(\frac{5}{6}\)=100(cm)
chu vi là:
(120+100)x2=440(cm)
diện tích là:
120x100=12000(cm2)
đáp số: chu vi:440 cm
diện tích:12000 cm2
11 tháng 1 2022
Do diện tích hình bình hành bằng diện tích của hình vuông cạnh 4 cm nên diện tích hình bình hành là:
4 x 4 = 16 (cm2)
Độ dài đáy hình bình hành là:
16 : 2 = 8 (cm)
Đáp số: 8 cm
29 tháng 4 2015
Chiều cao của hình bình hành đó là :
120 / 6 * 5 = 100 ( cm )
Chu vi của hình bình hành đó là :
( 120 + 100 ) * 2 = 440 ( cm )
Diện tích của hình bình hành đó là :
120 * 100 = 12000 ( cm2 )
ĐS : ........
24 tháng 10 2016
Chiều cao của hình bình hành là:
120 . 5 : 6 = 100 ( cm )
Chu vi của hình bình hành đó là:
( 120 + 100 ) . 2 = 440 ( cm )
Vậy ...
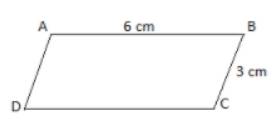
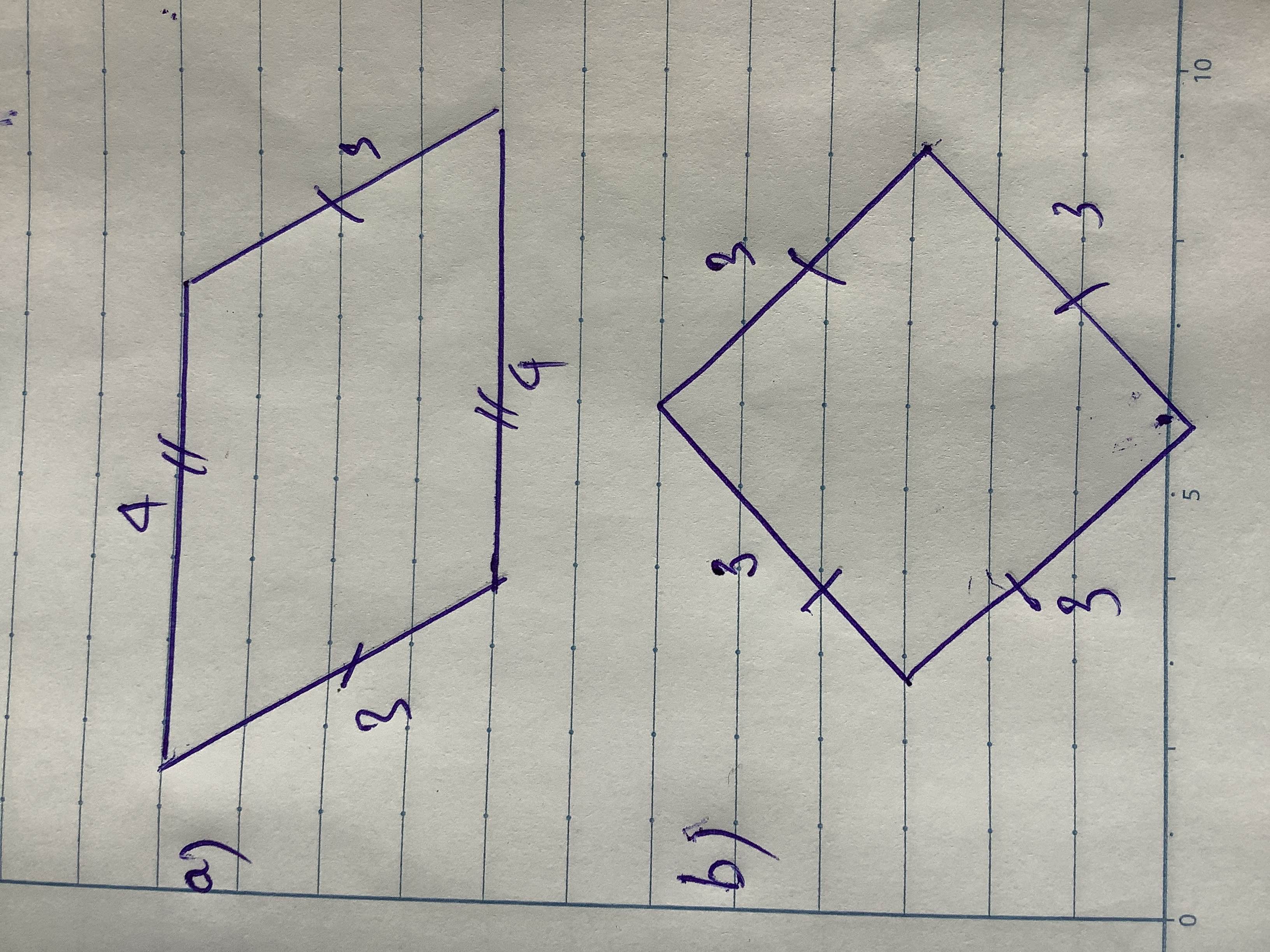
Bước 1. Vẽ đoạn thẳng AB = 6 cm.
Bước 2. Vẽ đường thẳng đi qua B. Trên đường thẳng đó lấy điểm C sao cho BC = 3 cm.
Bước 3. Vẽ đường thẳng đi qua A và song song với BC, đường thẳng qua C và song song với AB. Hai đường thẳng này cắt nhau tại D, ta được hình bình hành ABCD.
TL
Lời giải:
Vẽ hình chữ nhật ABCD có một cạnh bằng 6 cm, một cạnh bằng 4 cm theo hướng dẫn sau:
Bước 1. Vẽ đoạn thẳng AB = 6 cm.
Bước 2. Vẽ đường thẳng vuông góc với AB tại A. Trên đường thẳng đó lấy điểm D sao cho AD = 4 cm.
Bước 3. Vẽ đường thẳng vuông góc với AB tại B. Trên đường thẳng đó lấy điểm C sao cho BC = 4 cm.
Bước 4. Nối D với C ta được hình chữ nhật ABCD.
HT