Cho Tam giác ABC.các tia phân giác của các góc B và C cắt nhau ở I.Tính góc BIC biết rằng A=m^0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:góc ABI= góc IBC(BI là tia phân giác của góc ABC)
Góc AIB=IBC=80*÷2=40*
Lại có:ACI=ICB=40*÷2=20*(vì CI là tia phân giác của ACB)
Xét tam giác BIC có:IBC+ICB+BIC=180*(tổng 3 góc của tam giác)
=>BIC=180*-(IBC+ICB)=180*-(40*+20*)=180*-60*=120*

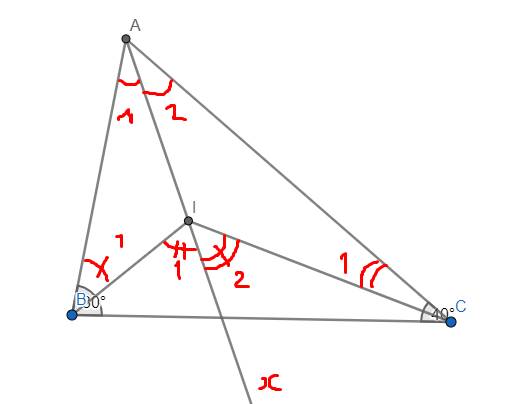
Ta có \(\widehat{I_1}=\widehat{A_1}+\widehat{B_1}\) và \(\widehat{I_2}=\widehat{A_2}+\widehat{C_1}\)
\(\Rightarrow\widehat{BIC}=\widehat{I_1}+\widehat{I_2}\)
\(=\left(\widehat{A_1}+\widehat{A_2}\right)+\left(\widehat{B_1}+\widehat{C_1}\right)\)
\(=\widehat{BAC}+\dfrac{\widehat{ABC}+\widehat{ACB}}{2}\)
\(=180^o-\left(\widehat{ABC}+\widehat{ACB}\right)+\dfrac{\widehat{ABC}+\widehat{ACB}}{2}\)
\(=180^o-\left(80^o+40^o\right)+\dfrac{80^o+40^o}{2}\)
\(=120^o\)
Vậy \(\widehat{BIC}=120^o\)
B1: Cho tam giác ABC có B=80, C=40 độ. Tia phân giác của góc B cắt AC tại D. Tính ADB.
B2: Cho ta giác ABC có B-C=20 độ. Đường phân giác AD của góc A cắt BC tại D. Tính ADB và ADC.
B3: Cho hình vẽ tính ACB

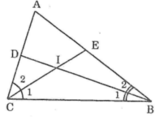
Ta có:
+ Trong ΔBIC có ∠BIC = 180o - (∠B1 + ∠C1) (1)
+ BI, CI là phân giác của ∠ABC và ∠BCA nên:
∠B1 = 1/2. ∠ABC; ∠C1 = 1/2. ∠ACB
⇒ ∠B1 + ∠C1 = 1/2. (∠ABC + ∠ACB) (2)
⇒ ∠ABC + ∠ACB = 180 - ∠A (3).
Từ (1), (2) và (3) suy ra ∠BIC = 180o - 1/2.(180 - ∠A) = 90o + 1/2.∠A
+) Nếu ∠A = 80o ⇒ ∠BIC = 90º + 1/2.80o = 130o.
+) Nếu ∠A = mo ⇒ ∠BIC = 90o + 1/2.mo.

Vì tam giác ABC là tam giác cân tại A nên B=C
Mà A=70 nên B+C=110
Suy ra B=C=110/2=55
Lại có B1=B2=55/2=27,5
góc C t/ư
Xét tam giác BICcos:
B2+BIC +C2=180(ĐL tổng 3 góc trong tam giác)
27,5+BIC+27,5=180
BIC=180-27,5-27,5
BIC=55
Vậy ...

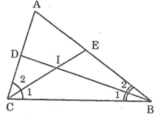
∠B = 80o, ∠C = 40o
Ta có:
∠(B1) = (1/2)∠(ABC) = (1/2).80o = 40o (vì BD là tia phân giác ∠(ABC))
∠(C1) = (1/2)∠(ACB) = (1/2).40o = 20o (vì CE là tia phân giác ∠(ACB))
Trong ΔIBC, ta có: ∠(BIC) + ∠(B1) + ∠(C1) = 180o(tổng 3 góc trong tam giác)
Vậy: ∠(BIC) = 180o - (∠(B1) + ∠(C1)) = 180o - (40o + 20o) = 120o
