Cho 2 số x,y thỏa mãn: x + 4y=1 . Tính giá trị nhỏ nhất của A=x^2 + 4y^2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HV
2
27 tháng 7 2023
\(A=\dfrac{1}{x}+\dfrac{1}{4y}=\dfrac{4}{4x}+\dfrac{1}{4y}=\dfrac{2^2}{4x}+\dfrac{1^2}{4y}\)
Áp dụng BĐT Cauchy schwart, ta có:
\(A=\dfrac{2^2}{4x}+\dfrac{1^2}{4y}\ge\dfrac{\left(2+1\right)^2}{4\left(x+y\right)}=\dfrac{9}{4.2}=\dfrac{9}{8}\)
Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{4x}=\dfrac{1}{4y}\\x+y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{2x}=\dfrac{1}{4y}\\x+y=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x=4y\\x+y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2y\\x+y=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{4}{3}\\y=\dfrac{2}{3}\end{matrix}\right.\)
Vậy, GTNN của \(A=\dfrac{9}{8}\Leftrightarrow\left(x,y\right)=\left(\dfrac{4}{3},\dfrac{2}{3}\right)\)
28 tháng 7 2023
Áp dụng BĐT Cosi cho 2 cặp số dương là \(\dfrac{1}{x};\dfrac{9}{16}x\) và \(\dfrac{1}{4y};\dfrac{9}{16}y\) , ta có:
\(\dfrac{1}{x}+\dfrac{9}{16}x\ge2\sqrt{\dfrac{1}{x}.\dfrac{9}{16}x}=2.\dfrac{3}{4}=\dfrac{3}{2}\)
\(\dfrac{1}{4y}+\dfrac{9}{16}y\ge2\sqrt{\dfrac{1}{4y}.\dfrac{9}{16}y}=2.\dfrac{3}{8}=\dfrac{3}{4}\)
Cộng vế theo vế ta được: \(\dfrac{1}{x}+\dfrac{1}{4y}+\dfrac{9}{16}\left(x+y\right)\ge\dfrac{3}{2}+\dfrac{3}{4}=\dfrac{9}{4}\)
\(\Leftrightarrow A+\dfrac{9}{16}.2\ge\dfrac{9}{4}\Leftrightarrow A\ge\dfrac{9}{4}-\dfrac{9}{8}=\dfrac{9}{8}\)
Dấu bằng xảy ra \(\Leftrightarrow\left(x,y\right)=\left(\dfrac{4}{3};\dfrac{2}{3}\right)\)
KS
1
19 tháng 3 2021
Toán lớp 0 ????? \(\text{ 🤔 }\text{ 🤔 }\text{ 🤔 }\text{ 😅 }\text{ 😅 }\text{ 😅 }\)
AH
Akai Haruma
Giáo viên
19 tháng 10 2024
Lời giải:
Áp dụng BĐT AM-GM:
$12=x^2+4+4y\geq 2\sqrt{4x^2}+4y=4x+4y=4(x+y)$
$\Rightarrow x+y\leq 3$
Tiếp tục áp dụng BĐT AM-GM:
$P=x+y+\frac{10}{x+y}=(x+y)+\frac{9}{x+y}+\frac{1}{x+y}$
$\geq 2\sqrt{(x+y).\frac{9}{x+y}}+\frac{1}{x+y}$
$=6+\frac{1}{x+y}\geq 6+\frac{1}{3}=\frac{19}{3}$ (do $x+y\leq 3$)
Vậy $P_{\min}=\frac{19}{3}$
Giá trị này đạt tại $x=2; y=1$
DM
0
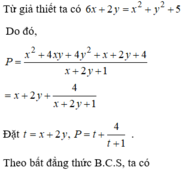
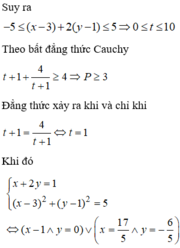
Bài này có thể áp dụng Bunhiacopxki nhưng đang lười nghĩ nên thôi vậy...
\(x+4y=1\Leftrightarrow x=1-4y\)
Khi đó : \(A=\left(1-4y\right)^2+4y^2\)
\(\Leftrightarrow A=16y^2-8y+1+4y^2\)
\(\Leftrightarrow A=20y^2-8y+1\)
\(\Leftrightarrow A=20\left(y^2-\frac{2}{5}y+\frac{1}{20}\right)\)
\(\Leftrightarrow A=20\left(y^2-2\cdot y\cdot\frac{1}{5}+\frac{1}{25}+\frac{1}{100}\right)\)
\(\Leftrightarrow A=20\left[\left(y-\frac{1}{5}\right)^2+\frac{1}{100}\right]\)
\(\Leftrightarrow A=20\left(y-\frac{1}{5}\right)^2+\frac{1}{5}\ge\frac{1}{5}\forall y\)
Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x=1-4y\\y=\frac{1}{5}\end{matrix}\right.\Leftrightarrow x=y=\frac{1}{5}\)