giups mình :((
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.







Lời giải:
a.
$8+x=20$
$x=20-8=12$
$A=\left\{12\right\}$
b.
$x+3<5$
$x< 5-3$
$x<2$. Vì $x$ là số tự nhiên nên $x$ có thể là $0,1$
$B=\left\{0;1\right\}$
c.
$x+0=x$ (luôn đúng với mọi $x\in\mathbb{N}$
$C=\left\{x=k| k\in\mathbb{N}\right\}$
d.
$25-x\leq 7$
$x\geq 25-7$
$x\geq 18$
$D=\left\{x=k|k\in\mathbb{N}, k\geq 18\right\}$
`@` `\text {Ans}`
`\downarrow`
`a)`
`8+x=20`
`=> x=20 - 8`
`=> x=12`
Vậy, `x=12`
`=> A = {12}`
`b)`
`x+3<5`
`=> x \in {0; 1}`
Vậy, `x \in {0; 1}`
`=> B = {0; 1}`
`c)`
`x+0=x`
`=> x=x (\text {luôn đúng})`
Vậy, `x` có vô giá trị `(x \in NN)`
`=> C = {x \in NN}`
`d)`
`25 - x \le 7`
`=> x \in {18; 19; 20; 21; 22; 23; 24; 25}`
`=> x \in {18 \le x \le 25}`
`=> D = {x \in NN` `|` `18 \le x le 25}`

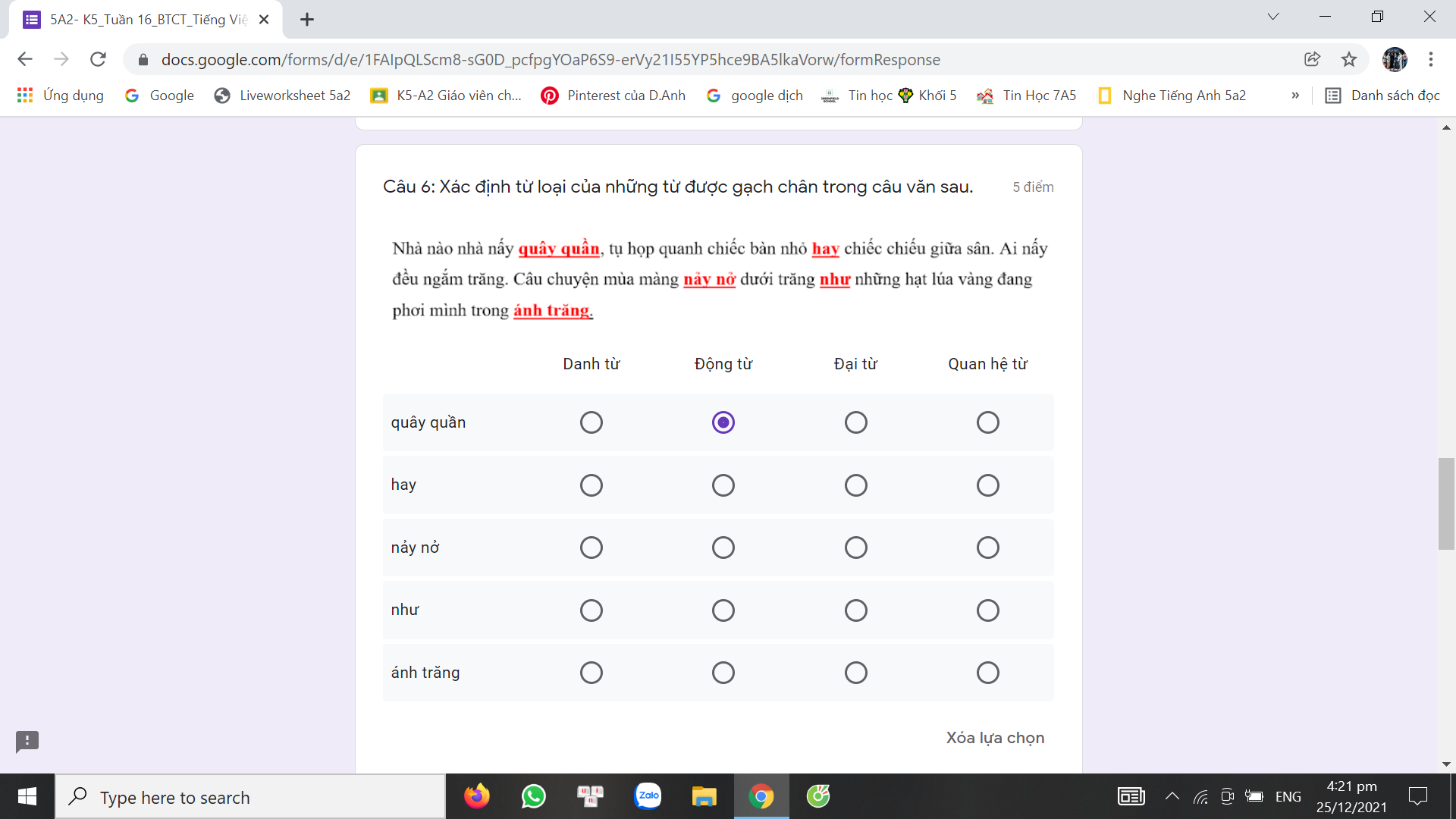
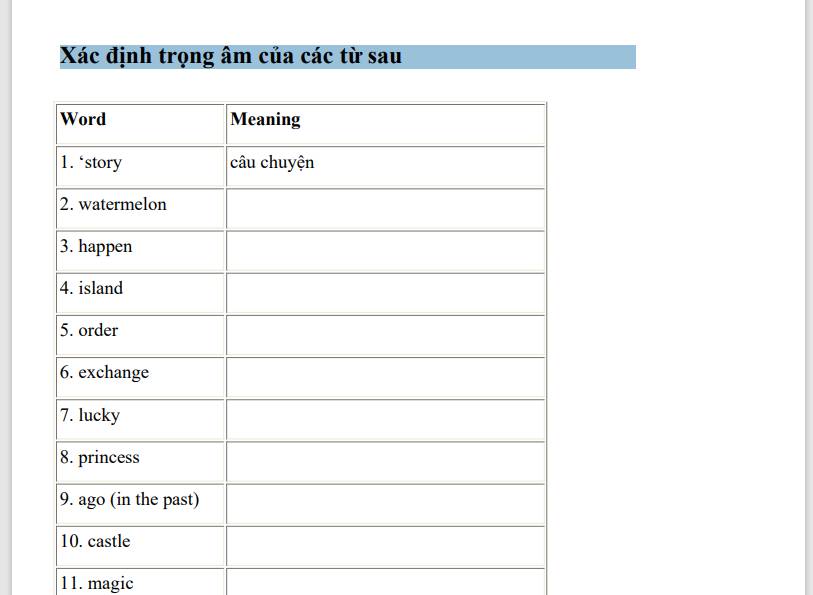
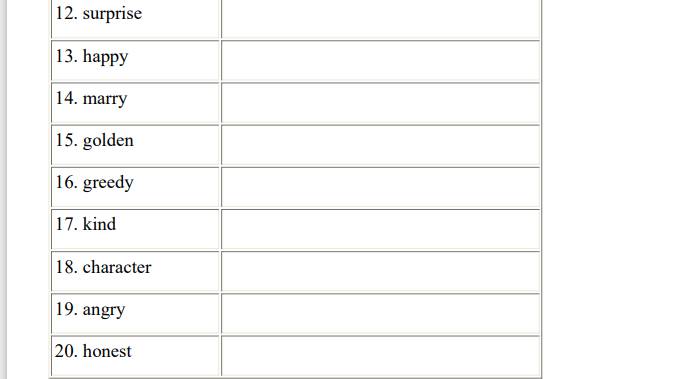

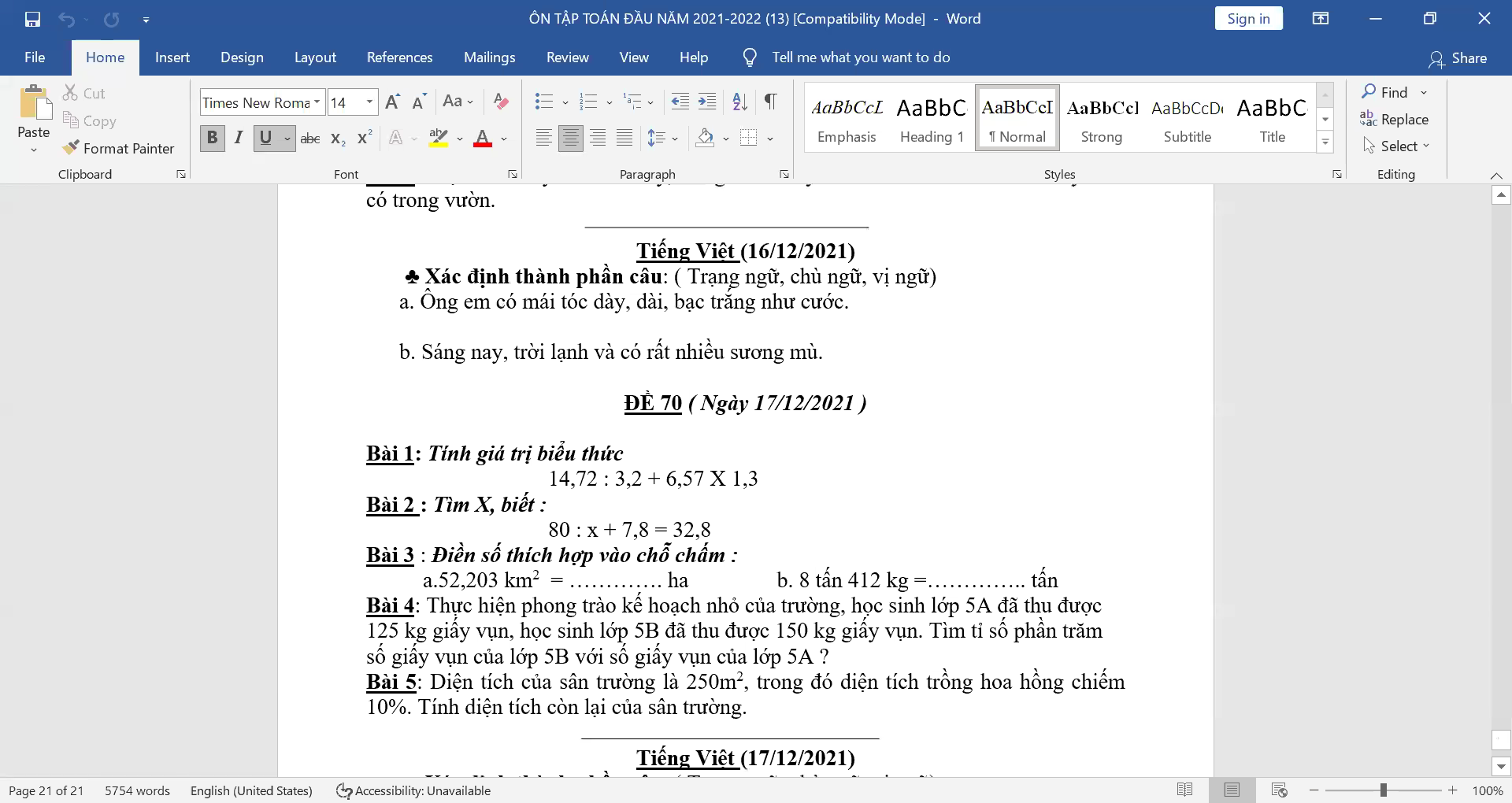
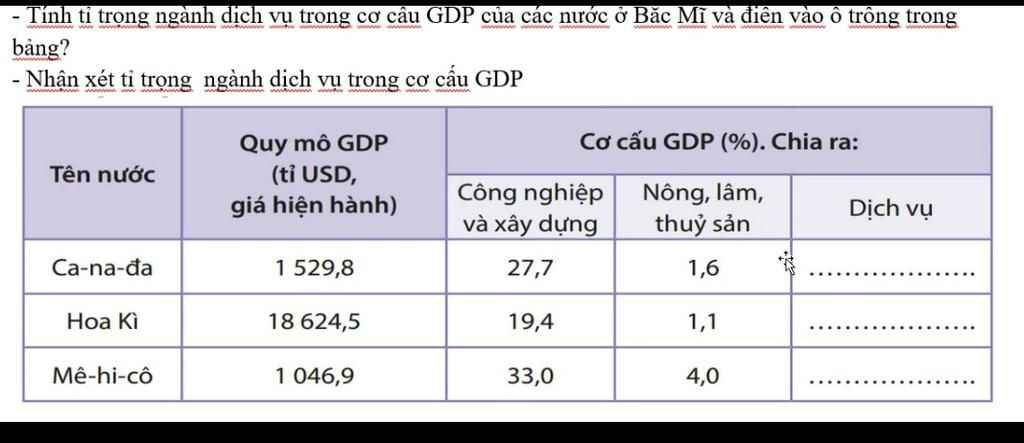 Giups mình với mình đang cần gấp j
Giups mình với mình đang cần gấp j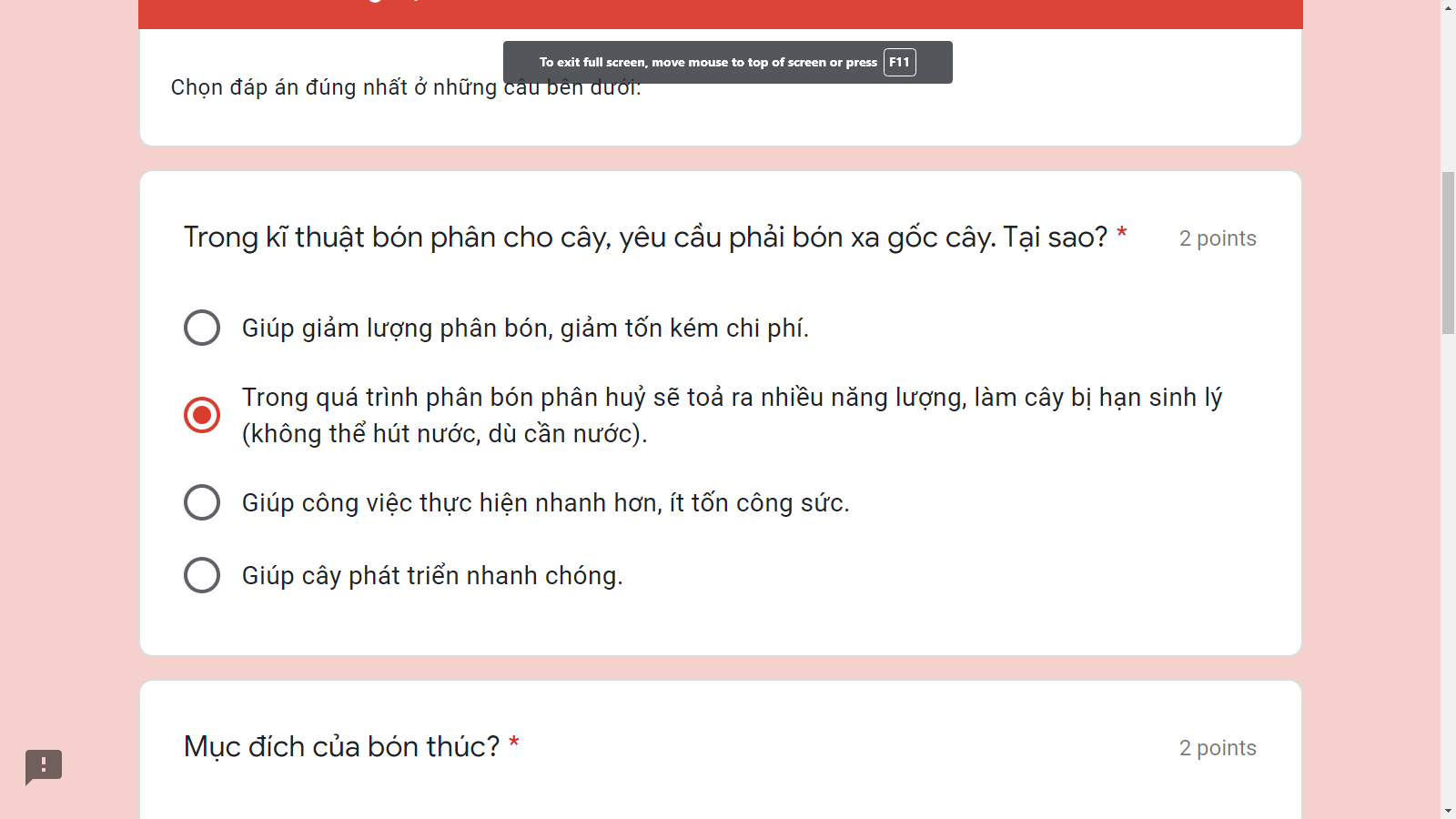


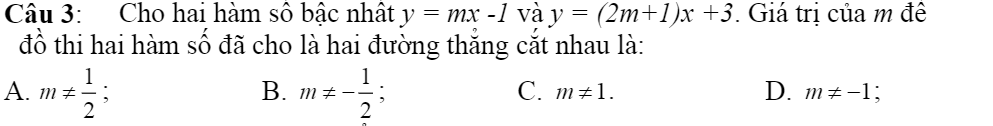
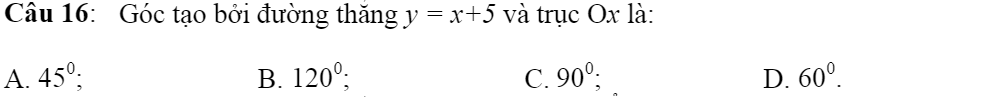
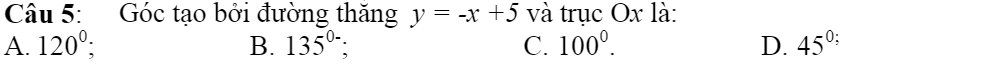
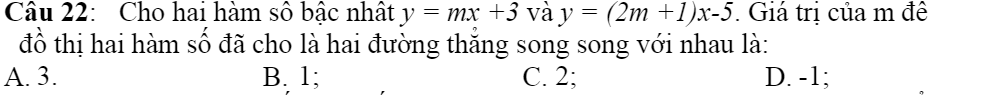
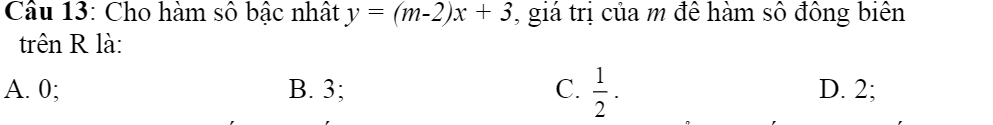
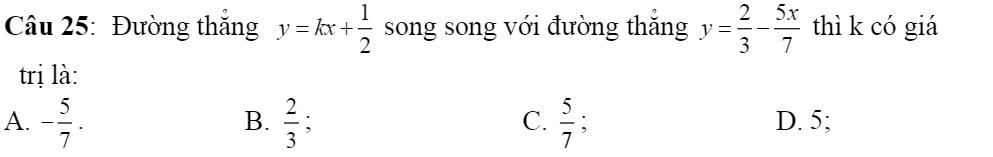

 Giups mình với
Giups mình với
Bài 1 :
a ) Đặt \(\frac{x}{3}=\frac{y}{8}=\frac{z}{5}=k\)
\(\Rightarrow\hept{\begin{cases}x=3k\\y=8k\\z=5k\end{cases}}\)
Thay vào ta có :
\(2.3k+3.8k-5k=50\)
\(6k+24k-5k=50\)
\(25k=50\)
\(k=2\)
\(\Rightarrow\hept{\begin{cases}x=3.2=6\\y=8.2=16\\z=5.2=10\end{cases}}\)
b ) Đặt \(\frac{x}{-3}=\frac{y}{5}=k\)
\(\Rightarrow\hept{\begin{cases}x=-3k\\y=5k\end{cases}}\)
Thay vào ta có :
\(\left(-3k\right)^2+\left(5k\right)^2=34\)
\(\left(-3\right)^2.k^2+5^2.k^2=34\)
\(9.k^2+25.k^2=34\)
\(34.k^2=34\)
\(k^2=1\)
\(k^2=1^2\)hoặc \(\left(-1\right)^2\)
\(k=\pm1\)
+ ) Nếu \(k=1\)\(\Rightarrow\hept{\begin{cases}x=-3.1=-3\\y=5.1=5\end{cases}}\)
+ ) Nếu \(k=-1\)\(\Rightarrow\hept{\begin{cases}x=\left(-3\right).\left(-1\right)=3\\y=5.\left(-1\right)=-5\end{cases}}\)
c ) Đặt \(\frac{x}{2}=\frac{y}{5}=k\)
\(\Rightarrow\hept{\begin{cases}x=2k\\y=5k\end{cases}}\)
Thay vào ta được :
\(2k.5k=10\)
\(10.k^2=10\)
\(k^2=1\)
\(k=\pm1\)
+ ) Nếu \(k=1\)\(\Rightarrow\hept{\begin{cases}x=2.1=2\\y=5.1=5\end{cases}}\)
+ ) Nếu \(k=-1\)\(\Rightarrow\hept{\begin{cases}x=2.\left(-1\right)=-2\\y=5.\left(-1\right)=-5\end{cases}}\)