Thang máy bắt đầu đi lên theo 3 giai đoạn : Giai đoạn 1: Nhanh dần đều không tốc độ đầu, với gia tốc 2m/s2 trong 1s Giai đoạn 2 : thẳng đều trong 5s Giai đoạn 3 : Chậm dần đều cho đến khi dừng lại hết 2s Tìm: a. Tốc độ của chuyển động thẳng đều? b. Quãng đường tổng cộng mà thang máy đi được?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TK
7 tháng 8 2021
Tóm tắt:
\(v_0=0\) m/s
v=4 m/s
\(t_0=0\) s
\(t_1=4\) s
\(t_2=5\) s
\(t_3=8\) s
\(s=?\)km
Giải
Gia tốc của thang máy trong giai đoạn 1 là
\(a=\dfrac{\Delta v}{\Delta t}=\dfrac{v-v_0}{t_1-t_0}=\dfrac{4-0}{4-0}=1\)(m/s2)
Quãng đường thang máy chuyển động trong giai đoạn 1 là
\(s_1=v_0t_1+\dfrac{1}{2}at_1^2=0\cdot4+\dfrac{1}{2}\cdot1\cdot4^2=8\left(m\right)\)
Quãng đường thang máy chuyển động trong giai đoạn 2 là
\(s_2=v\cdot t_2=4\cdot5=20\left(m\right)\)
Gia tốc của thang máy trong giai đoạn 2 là
\(a'=\dfrac{\Delta v'}{\Delta t'}=\dfrac{v-v_0}{t_3}=\dfrac{4-0}{8}=\dfrac{1}{2}\)(m/s2)
Quãng đường thang máy chuyển động trong giai đoạn 3 là
\(s_3=v_0t_3+\dfrac{1}{2}a't_3^2=0\cdot8+\dfrac{1}{2}\cdot\dfrac{1}{2}\cdot8^2=16\left(m\right)\)
Quãng đường di chuyển dc của thang máy là
\(s_1+s_2+s_3=8+20+16=44\left(m\right)\)
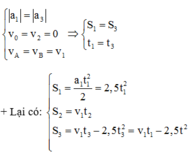
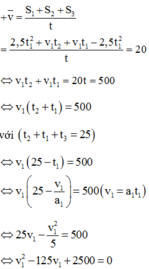
a) v1 = v01 + a1 . t = 2t
t1 = 1 (s) => v2 = v1 = 2 . 1 = 2(m/s)
b) s1 = v01 . t + 1/2 . a1 . t^2 = 0 . 1 + 1/2 . 2 . 1^2 = 1 (m)
s2 = v02 . t ( t = t2 = 5s )
= 2 . 5 = 10 (m)
a03 = ( v3 - v03 ) / t3
= ( 0 - 2 ) / 2
= -1 (m/s)
=> s3 = v03 . t + 1/2 .a3 .t^2 (t=t3=2s)
= 2 . 2 + 1/2 . (-1) . 2^2
= 2 (m)
==> S = s1 + s2 + s3
= 1 + 10 + 2
= 13 (m)
Tham thảo :
a) v1 = v01 + a1 . t = 2t
t1 = 1 (s) => v2 = v1 = 2 . 1 = 2(m/s)
b) s1 = v01 . t + 1/2 . a1 . t^2 = 0 . 1 + 1/2 . 2 . 1^2 = 1 (m)
s2 = v02 . t ( t = t2 = 5s )
= 2 . 5 = 10 (m)
a03 = ( v3 - v03 ) / t3
= ( 0 - 2 ) / 2
= -1 (m/s)
=> s3 = v03 . t + 1/2 .a3 .t^2 (t=t3=2s)
= 2 . 2 + 1/2 . (-1) . 2^2
= 2 (m)
==> S = s1 + s2 + s3
= 1 + 10 + 2
= 13 (m)