chứng minh rằng hai tam giác ABC và A'B'C' có cùng trọng tâm ⇌ \(\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}=0\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Xét tam giác ADC và tam giác BEC ta có
^C _ chung
^ADC = ^BEC = 900
Vậy tam giác ADC ~ tam giác BEC (g.g)
b, => ^DAC = ^EBC ( 2 góc tương ứng )
Xét tam giác HAE và tam giác HBD ta có
^AHE = ^BHD ( đối đỉnh )
^HAE = ^HBD (cmt)
Vậy tam giác HAE ~ tam giác HBD (g.g)
\(\dfrac{AH}{HB}=\dfrac{HE}{DH}\Rightarrow AH.DH=HE.HB\)

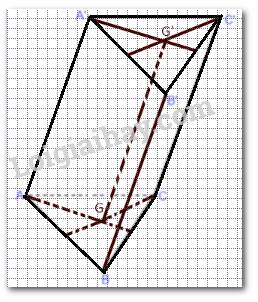
a) Ta có ABC.A'B'C' là hình lăng trụ nên \(\Delta ABC = \Delta A'B'C'\) suy ra AG = A'G'.
Lại có (ABC) // (A'B'C'), giao tuyến của mp(AGG'A') với (ABC) và (A'B'C') lần lượt là AG, A'G' suy ra AG // A'G'.
Như vậy , tứ giác AGG'A' có AG = A'G', AG // A'G' là hình bình hành.
b) AGG'A' là hình bình hành suy ta AA' // GG'.
Lại có AA' // CC' (do ABC.A'B'C' là hình lăng trụ).
Mặt phẳng (AGC) // (A'G'C') suy ra AGC.A'G'C' là hình lăng trụ.

a: góc AEB=góc AHB=90 độ
=>ABHE nội tiếp
b: góc HED=góc ABC=1/2*sđ cung AC=góc ADC
=>HE//CD

a: Do AC > A'C' nên lấy được điểm C1 trên cạnh AC sao cho AC1=A′C′.
Ta có ΔABC1=ΔA'B'C'
Suy ra B′C′=BC1
Mặt khác hai đường xiên BC và BC1 kẻ từ B đến đường thẳng AC lần lượt có hình chiếu trên AC là AC và AC1.
Vì AC > AC1 nên BC > BC1.
Suy ra BC > B'C'.
b:
-Giả sử AC<A'C'.
Khi đó theo chứng minh câu a) ta có BC < B'C'. Điều này không đúng với giả thiết BC > B'C'.
Giả sử AC=A'C'. Khi đó ta có ΔABC=ΔA'B'C' (c.g.c).
Suy ra BC=B'C'.
Điều này cũng không đúng với giả thiết BC>B'C'. Vậy ta phải có AC>A'C'.

A B C D
a) Xét ABD và EBD có
BD cạnh chung
BAD=BED(=90)
ABD=EBD(vì BD là tia phân giác của B)
b ko biet
b)Vì theo ý a) BAD=BED và BD là tia phân giác của B. Nên ADE là tam giác cân

Lời giải:
Bổ đề: Tam giác $ABC$ có trọng tâm $G$
\(\Leftrightarrow \overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
Chứng minh:
* Chiều thuận:
Kéo dài $AG$ cắt $BC$ tại $M$ thì $M$ là trung điểm $BC$ nên $\overrightarrow{BM}+\overrightarrow{CM}=\overrightarrow{0}$
Ta có: \(\overrightarrow{GM}=\overrightarrow{GB}+\overrightarrow{BM};\overrightarrow{GM}=\overrightarrow{GC}+\overrightarrow{CM}\)
\(\Rightarrow 2\overrightarrow{GM}=\overrightarrow{GB}+\overrightarrow{BM}+\overrightarrow{GC}+\overrightarrow{CM}=\overrightarrow{GB}+\overrightarrow{GC}\)
Mà theo tính chất trọng tâm: \(-\overrightarrow{GA}=2\overrightarrow{GM}\)
\(\Rightarrow -\overrightarrow{GA}=\overrightarrow{GB}+\overrightarrow{GC}\) \(\Rightarrow \overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
* Chiều đảo:
Gọi $M,N$ là trung điểm của $BC,AC$
Vì \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\Leftrightarrow \overrightarrow{GA}+(\overrightarrow{GM}+\overrightarrow{MB})+(\overrightarrow{GM}+\overrightarrow{MC})=\overrightarrow{0}\)
\(\Leftrightarrow \overrightarrow{GA}+2\overrightarrow{GM}=\overrightarrow{0}\Rightarrow \overrightarrow{GA}=-2\overrightarrow{GM}\) nên $G,A,M$ thẳng hàng.
Tương tự: $G,B,N$ thẳng hàng nên $G$ là trọng tâm tam giác $ABC$
Ta có đpcm.
----------------------------------------------
Áp dụng vào bài:
$G$ là trọng tâm của $ABC$ và $A'B'C'$
\(\Leftrightarrow \overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}=\overrightarrow{GA'}+\overrightarrow{GB'}+\overrightarrow{GC'}\)
\(\Leftrightarrow \overrightarrow{GA'}-\overrightarrow{GA}+\overrightarrow{GB'}-\overrightarrow{GB}+\overrightarrow{GC'}-\overrightarrow{GC}=\overrightarrow{0}\)
\(\Leftrightarrow \overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}=\overrightarrow{0}\)
Cách khác:
Gọi \(G,G'\)lần lượt là trọng tâm của \(\Delta ABC,\Delta A'B'C'\) ,ta có:
\(3\overrightarrow{GG'}=\overrightarrow{GA'}+\overrightarrow{GB'}+\overrightarrow{GC'}\)
\(3\overrightarrow{GG'}=\left(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right)+\left(\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}\right)\)
\(G\) là trọng tâm của \(\Delta ABC\) \(\Rightarrow\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
\(\Rightarrow3\overrightarrow{GG'}=\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}\)
Để hai tam giác ABC và A'B'C' có trọng tâm trùng nhau \(\Rightarrow\overrightarrow{GG'}=\overrightarrow{0}\)
\(\Rightarrow3\overrightarrow{GG'}=\overrightarrow{0}\Leftrightarrow\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}=\overrightarrow{0}\)(đpcm)