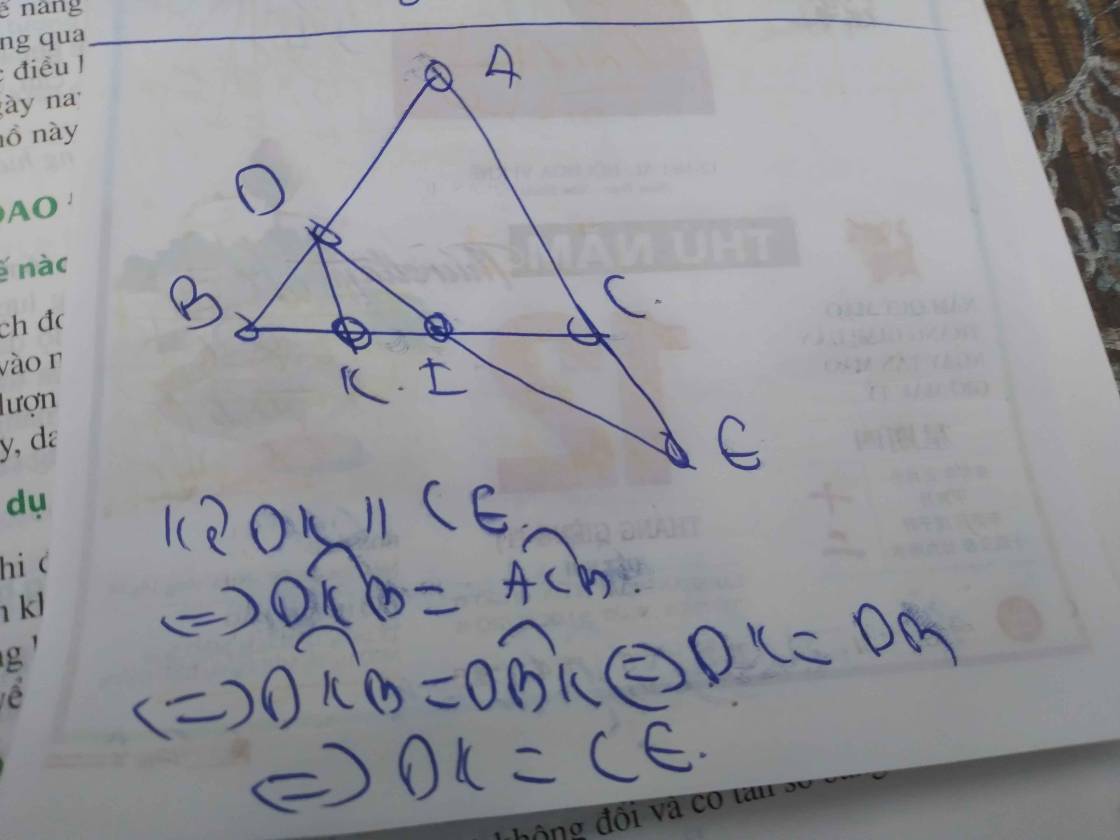
Cho 🔺ABC điểm D thuộc cạnh AC ,điểm E thuộc cạnh AB sao cho CD=1/4 CA, BE=1/3 BA .Gọi O là giao điểm của BD và CE .CM : OE = OC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 4 2018
a)
Xét tam giác ADC và tam giác AEB có :
AD = AE (GT)
Góc A chung
AC = AB ( vì tam giác ABC cân )
từ 3 điều trên => tam giác ADC = tam giác AEB (c-g-c )
=> DC= BE ( cặp cạnh tương ứng )
b) vì tam giác ADC = tan giác AEB ( câu a )
=> góc ABE = góc ACD ( cặp góc tương ứng )
ta có : tam giác ABC cân => AB = AC (1)
và AD = AE (GT ) (2)
từ (1) và (2) => BD = CE
Xét tam giác KBD và tam giác KCE Có :
góc DKB = góc EKC ( 2 góc đối đỉnh )
BD = CE ( chứng minh trên )
Góc DKB = góc EKC ( đối đỉnh )
từ 3 điều trên => tam giác KBD = tam giác KCE ( g-c-g )
14 tháng 8 2021
a: Xét ΔBEC có
I là trung điểm của BE
M là trung điểm của BC
Do đó: IM là đường trung bình của ΔBEC
Suy ra: \(IM=\dfrac{EC}{2}\left(1\right)\)
Xét ΔDCB có
K là trung điểm của DC
M là trung điểm của BC
Do đó: KM là đường trung bình của ΔDCB
Suy ra: \(KM=\dfrac{BD}{2}\)
mà BD=CE
nên \(KM=\dfrac{CE}{2}\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra IM=KM
23 tháng 2 2022
a: Xét ΔABE và ΔACD có
AB=AC
\(\widehat{BAE}\) cung
AE=AD
Do đó: ΔABE=ΔACD
Suy ra: BE=CD
b: Xét ΔDBC và ΔECB có
DB=EC
DC=EB
BC chung
Do đó: ΔDBC=ΔECB
Xét ΔHDB và ΔHEC có
\(\widehat{HDB}=\widehat{HEC}\)
DB=EC
\(\widehat{HBD}=\widehat{HCE}\)
Do đó:ΔHBD=ΔHCE
c: Ta có: ΔHBD=ΔHCE
nên HB=HC
Xét ΔABH và ΔACH có
AB=AC
AH chung
BH=CH
DO đó ΔABH=ΔAHC
Suy ra: \(\widehat{BAH}=\widehat{CAH}\)
hay AH là tia phân giác của góc BAC
d:Ta có: ΔABC cân tại A
mà AH là đường phân giác
nên AH là đường cao
e: Xét ΔABC có AD/AB=AE/AC
nên DE//BC
