Cho hàm số y = \(\sqrt{x^2-2x+1}\)+ \(\sqrt{x^2-6x+9}\)
vẽ đồ thị hàm số trên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 7 2021
\(y=\left|x+1\right|+\sqrt{\left(x-2\right)^2}=\left|x+1\right|+\left|x-2\right|\)
\(\Rightarrow\left\{{}\begin{matrix}y=2x-1\text{ với }x\ge2\\y=1-2x\text{ với }x\le-1\\y=3\text{ với }-1\le x\le2\end{matrix}\right.\)
Từ đó ta có đồ thị hàm số như sau (vẽ 3 đồ thị hàm bậc nhất xác định trên trên ở từng khoảng của chúng)
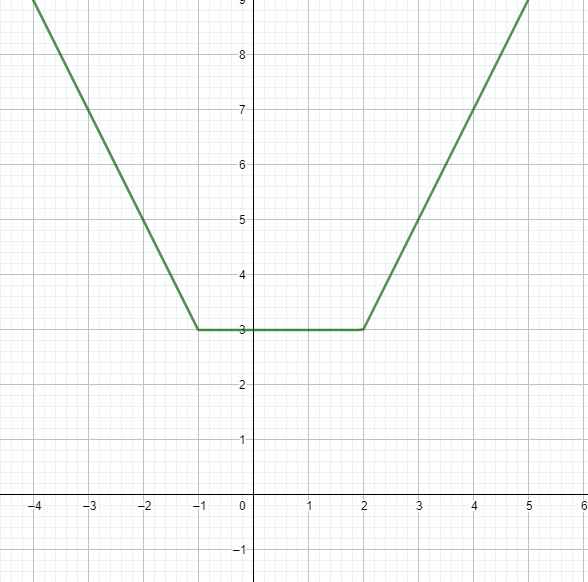
Từ đồ thị \(\Rightarrow y_{min}=3\) khi \(-1\le x\le2\)
10 tháng 4 2021
Câu 1:
1: Ta có: \(16\sqrt{9}-9\sqrt{16}\)
\(=16\cdot3-9\cdot4\)
\(=48-36=12\)
10 tháng 4 2021
2:
a) Thay x=2 và y=8 vào hàm số \(y=a\cdot x^2\), ta được:
\(a\cdot2^2=8\)
\(\Leftrightarrow4a=8\)
hay a=2
Vậy: a=2
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 8 2021
1.
Điều kiện xác định của căn thức: \(\left[{}\begin{matrix}x\ge3\\x\le-3\end{matrix}\right.\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{x^2+1}-x}{\sqrt{x^2-9}-4}=\dfrac{1-1}{1}=0\Rightarrow y=0\) là 1 TCN
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\sqrt{x^2+1}-x}{\sqrt{x^2-9}-4}=\dfrac{-1-1}{-1}=2\Rightarrow y=2\) là 1 TCN
\(\lim\limits_{x\rightarrow-5}\dfrac{\sqrt{x^2+1}-x}{\sqrt{x^2-9}-4}=\dfrac{\sqrt{26}+5}{0}=+\infty\Rightarrow x=-5\) là 1 TCĐ
\(\lim\limits_{x\rightarrow5}\dfrac{\sqrt{x^2+1}-x}{\sqrt{x^2-9}-4}=\dfrac{\sqrt{26}-5}{0}=+\infty\Rightarrow x=5\) là 1 TCĐ
Hàm có 4 tiệm cận
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 8 2021
2.
Căn thức của hàm luôn xác định
Ta có:
\(\lim\limits_{x\rightarrow2}\dfrac{2x-1-\sqrt{x^2+x+3}}{x^2-5x+6}=\lim\limits_{x\rightarrow2}\dfrac{\left(2x-1\right)^2-\left(x^2+x+3\right)}{\left(x-2\right)\left(x-3\right)\left(2x-1+\sqrt{x^2+x+3}\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(3x+1\right)}{\left(x-2\right)\left(x-3\right)\left(2x-1+\sqrt{x^2+x+3}\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{3x+1}{\left(x-3\right)\left(2x-1+\sqrt{x^2+x+3}\right)}=\dfrac{-7}{6}\) hữu hạn
\(\Rightarrow x=2\) ko phải TCĐ
\(\lim\limits_{x\rightarrow3}\dfrac{2x-1-\sqrt{x^2+x+3}}{x^2-5x+6}=\dfrac{5-\sqrt{15}}{0}=+\infty\)
\(\Rightarrow x=3\) là tiệm cận đứng duy nhất
AH
Akai Haruma
Giáo viên
15 tháng 11 2021
Bài 1:
a. Để $(d)$ đi qua $A(-1;3)$ thì:
$y_A=2x_A+m\Leftrightarrow 3=2(-1)+m$
$\Leftrightarrow m=5$
b. Để $(d)$ đi qua $B(\sqrt{2}; -5\sqrt{2})$ thì:
$y_B=2x_B+m$
$\Leftrightarrow -5\sqrt{2}=2\sqrt{2}+m$
$\Leftrightarrow m=-7\sqrt{2}$
\(y=\sqrt{x^2-2x+1}+\sqrt{x^2-6x+9}=\sqrt{\left(x-1\right)^2}+\sqrt{\left(x-3\right)^2}\)
\(\Rightarrow y=\left|x-1\right|+\left|x-3\right|\)
- Xét \(x=0\Rightarrow y=\left|0-1\right|+\left|0-3\right|=\left|-1\right|+\left|-3\right|=4\)
- Xét \(y=0\Rightarrow\left|x-1\right|+\left|x-3\right|=0\Leftrightarrow\left|x-1\right|=\left|x-3\right|\)
\(\Rightarrow1\le x< 3\Leftrightarrow x-1=3-x\Leftrightarrow x=2\) (thỏa)
Vậy đồ thị hàm số đi qua \(A\left(0;4\right)\) và \(B\left(2;0\right)\)
---------------Tự vẽ nhé-------------------
thanks