Cho tam giác ABC có ba góc nhọn. Các đường cao AD, BE, CF và trực tâm H. Chứng minh:
a) Các điểm A, C, D, F nằm trên một đường tròn.
b) Các điểm A, E, H, F nằm trên một đường tròn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(OE=OB=\dfrac{1}{2}BC\Rightarrow\widehat{OBE}=\widehat{OEB}\)
\(\widehat{AHE}=\widehat{BHO}\) ; \(\widehat{BHO}+\widehat{HBD}=90^0\)
\(\Rightarrow\widehat{AHE}+\widehat{HBD}\left(\widehat{OBE}\right)=90^0\)
\(\Rightarrow\widehat{AHE}+\widehat{OEB}=90^0\)
\(IE=IH=r\Rightarrow\widehat{AHE}=\widehat{IEH}\)
\(\Rightarrow\widehat{IEH}+\widehat{OEB}=90^0\Rightarrow IE\perp OE\)

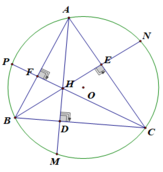
b) Xét tứ giác BFEC có:
∠(BFC) = 90 0 (Do CF là đường cao)
∠(BEC ) = 90 0 (Do BE là đường cao)
⇒ E và F cùng nhìn BC dưới một góc bằng nhau
⇒ Tứ giác BFEC nội tiếp được đường tròn
⇒ Bốn điểm B, E, F, C cùng nằm trên đường tròn

a: góc AEB=góc AHB=90 độ
=>AEHB nội tiếp
Xét ΔAHB vuông tại H và ΔACD vuông tại C có
góc ABH=góc ADC
=>ΔAHB đồng dạng với ΔACD
b: góc HAC+góc AHE
=góc ABE+90 độ-góc HAB
=90 độ
=>HE vuông góc AC
=>HE//CD

Đáp án:
Giải thích các bước giải:
1. Xét tứ giác CEHD có :
CEH = 90 ( BE là đường cao )
CDH = 90 ( AD là đường cao )
⇒ CEH + CDH = 90 + 90 = 180
Mà CEH và CDH là hai góc đối của tứ giác CEHD
⇒ CEHD là tứ giác nội tiếp (đpcm)
2. BE là đường cao ( gt )
⇒ BE ⊥ AB ⇒ BFC = 90
Như vậy E và F cùng nhìn BC dưới một góc 90 ⇒ E và F cùng nằm trên (O) đường kính AB
⇒ 4 điểm B, C, E, F cùng nằm trên một đường tròn (đpcm)
3. Xét ΔAEH và ΔADC có :
AEH = ADC (=90)
A chung
⇒ ΔAEH ~ ΔADC
⇒ AE/AD = AH/AC
⇒ AE.AC = AH.AD
Xét ΔBEC và ΔADC có :
BEC = ADC (=90)
C chung
⇒ ΔBEC ~ ΔADC
⇒ AE/AD = BC/AC
⇒ AD.BC = BE.AC (đpcm)
4. Có : C1 = A1 (cùng phụ góc ABC)
C2 = A1 ( hai góc nối tiếp chắn cung BM )
⇒ C1 = C2 ⇒ CB là tia phân giác HCM
Lại có : CB ⊥ HM
⇒ Δ CHM cân tại C
⇒ CB là đường trung trực của HM
⇒ H và M đối xứng nhau qua BC (đpcm)
5. Có : Bốn điểm B,C,E,F cùng nằm trên một đường tròn ( câu 2 )
⇒ C1 = E1 (hai góc nội tiếp cùng chắn BF) (*)
Có : Tứ giác CEHD nội tiếp (câu 1)
⇒ C1 = E2 (hai góc nội tiếp cùng chắn cung HD ) (**)
Từ (*) và (**) ta suy ra :
E1 = E2
⇒ EB là tia phân giác DEF
Cm tương tự ta được : FC là tia phân giác của DFE
Mà BE và CF cắt nhau tại H
⇒ H là tâm của đường tròn nội tiếp ΔDEF

a: Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
=>BFEC là tứ giác nội tiếp
=>B,F,E,C cùng thuộc một đường tròn
b: Xét ΔAHE vuông tại E và ΔACD vuông tại D có
\(\widehat{HAE}\) chung
Do đó: ΔAHE đồng dạng với ΔACD
=>\(\dfrac{AH}{AC}=\dfrac{AE}{AD}\)
=>\(AH\cdot AD=AC\cdot AE\)
Xét ΔABC có AD là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot AD\cdot BC\left(1\right)\)
Xét ΔABC có BE là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot BE\cdot AC\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{1}{2}\cdot AD\cdot BC=\dfrac{1}{2}\cdot BE\cdot AC\)
=>\(AD\cdot BC=BE\cdot AC\)
Xét tứ giác AFDC có:
AFC =90 , ADC=90(gt)
mà 2 góc này cùng nhìn cạnh AC
nên tứ giác AFDC nội tiếp đường tròn đường kính AC hay A,C,D,F cùng thuộc một đường tròn
Xét tứ giác AEHF có"
AFH =90 AEH=90(gt)
AFH+AEH =180
mà 2 góc này nằm ở vị trí đối nhau
nên tứ giác AEHF nội tiếp đường tròn đường kính AH
hay A,F,H,E cùng thuộc một đường tròn