Cho đường tròn (O) và một điểm A trên đường tròn đó. Trên đoạn OA lấy điểm B sao cho OB= 1/3 OA. Vẽ đường tròn đường kính AB.
a) Chứng minh đường tròn đường kính AB tiếp xúc với đường tròn (O) cho trước.
b) Vẽ đường tròn đồng tâm (O) với đường tròn (O) cho trước, căt đường tròn đường kính AB tại C. Tia AC cắt hai đường tròn đồng tâm tại D và E ( D nằm giữa C và E). Chứng minh AC=CD=DE

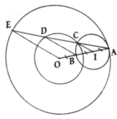
Ai giúp mình với mình nợ bài này lâu quá r
a) Gọi d là tiếp tuyến tại A của đường tròn (O) => d vuông góc OA => d vuông góc AB
Vì AB là đường kính của đường tròn (AB) nên d cũng là tiếp tuyến của (AB)
Vậy (O) và (AB) tiếp xúc nhau tại A (đpcm).
b) Gọi I là trung điểm đoạn AB => I là tâm của (AB) => ^ICA = ^IAC = ^OEA => IC // OE
Ta thấy OB = BI = IA = OA/3 => \(\frac{AI}{AO}=\frac{1}{3}\). Áp dụng ĐL Thales vào \(\Delta\)AEO có
\(\frac{AC}{AE}=\frac{AI}{AO}=\frac{1}{3}\) => AC = 1/3.AE (1)
Gọi OC,OD cắt đường tròn (O) cho trước lần lượt tại F,G. Khi đó DC // GF
Hay GF // AE. Mà GF và AE là các dây của đường tròn (O) nên (GE = (AF => ^EOG = ^AOF
Xét \(\Delta\)ODE và \(\Delta\)OCA: OD = OC, ^EOD = ^AOC (cmt), OE = OA => \(\Delta\)ODE = \(\Delta\)OCA (c.g.c)
=> ED = AC. Kết hợp với (1) suy ra AC = DE = AE/3 => AC = CD = DE (đpcm).