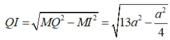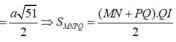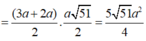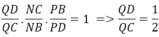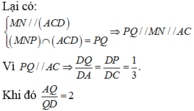VẼ HÌNH NHA
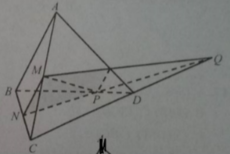
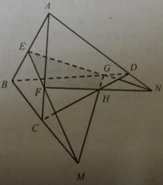
Câu 1. Cho tứ diện ABCD có M, N lần lượt là trung điểm AB, BC. P thuộc BD sao cho PB = 2PD. Tìm giao điểm của AC và (MNP); BD và (MNP)
Câu 2. cho hình chóp SABCD có đáy là hình bình tâm O. Gọi M,N lần lượt là trung điểm của SB,AD G là trọng tâm tam giác SAD. tìm giao điểm (VẼ HÌNH NHA )
a, GM và ABCD
b, AD và OMG
c, SA và OMG
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có M là điểm chung thứ nhất.
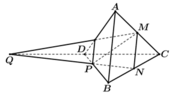
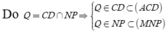
=> Q là điểm chung thứ hai.
Vậy ![]()
Chọn B.

NP là đường trung bình của ∆ACD ⇒ NP // AB, mà AB ⊂ (ABC) ⇒NP // (ABC)
P ∈ (MNP) ∩ (ACD) (1)
Trong mặt phẳng (BCD) gọi J = MN ∩ CD, có
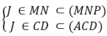
J ∈ (MNP) ∩ (ACD) (2)
Từ (1) và (2) : (MNP) ∩ (ACD) = JP
Trong mặt phẳng (ACD) gọi Q = JP ∩ AC. Có:
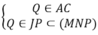
⇒ Q = AC ∩ (MNP). Có:
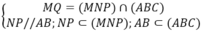
⇒MQ // NP // AB
Theo định lí Ta – lét có
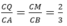
Kết luận:
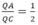
Đáp án A

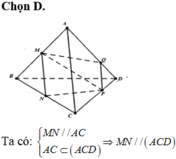
Đáp án là D
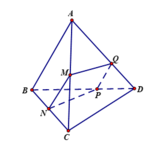
Trong mặt phẳng (ABD) qua P kẻ đường thẳng song song AB cắt AD tại Q ta có
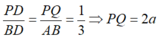
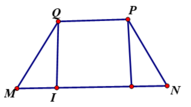
Dễ thấy MN là đường trung bình tam giác ABC nên MN//AB//PQ,nên 4 điểm M,N,P,Q đồng phẳng và MN=3a, thiết diện cần tim chính là hinh thang MNPQ, do tất cả các cạnh cạnh của tứ diện bằng 6a nên tam giác BNP = tam giác AMQ => NP = MQ vậy MNPQ là hình thang cân, ta có
![]()
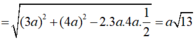
Kẻ đường cao QI có