Tìm nghiệm nguyên của phương trình x4 - y4 = 3y2 + 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 7 2021
\(x^4+y^4=3y^2+1\Leftrightarrow-y^4+3y^2+1=x^4\ge0\)
\(\Rightarrow-y^4+3y^2+1\ge0\Rightarrow\frac{3-\sqrt{13}}{2}\le y^2\le\frac{3+\sqrt{13}}{2}\)
Mà \(y\in Z\Rightarrow y^2\)là số chính phương \(\Rightarrow y^2=0;1\)
*\(y^2=0\Rightarrow x^4=1\Rightarrow x=-1;1\)
*\(y^2=1\Rightarrow x^4+1=3+1\Rightarrow x^4=3\Rightarrow x\notin Z\)
Vậy phương trình có nghiệm nguyên \(\left(-1;0\right),\left(1;0\right)\)
PH
0
15 tháng 1 2022
Ta có x4 + x2 + 1 = y2
Lại có x4 + 2x2 + 1 ≥ x4 + x2 + 1 hay (x2 + 1)2 ≥ x4 + x2 + 1
=> (x2 + 1)2 ≥ y2 (1)
Lại có x4 + x2 + 1 > x4 => y2 > x4 (2)
Từ (1) và (2), ta có x4 < y2 ≤ (x2 + 1)2
<=> y2 = (x2 + 1)2 = x4 + 2x2 + 1
Mà x4 + x2 + 1 = y2 => x4 + 2x2 + 1 = x4 + x2 + 1
<=> x2 = 0 <=> x = 0
Thay vào, ta có 1 = y2 <=> y ∈ {-1,1}
Vậy ...
BN
0
27 tháng 12 2021
\(2x^2+5xy+3y^2\\= 2x^2+2xy+3xy+3y^2\\= 2x\left(x+y\right)+3y\left(x+y\right)\\=\left(2x+3y\right)\left(x+y\right) \)
27 tháng 12 2021
2x^2-5xy-3y^2
= 2^x + xy - 6xy - 3y^2
= x(2x + y) - 3y(2x + y)
= (2x + y)(x - 3y)
DH
0
DH
0
LT
0
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 1
\(\Leftrightarrow x^2+3xy+3y^2+xy-2x-6y=5\)
\(\Leftrightarrow x\left(x+3y\right)+y\left(x+3y\right)-2\left(x+3y\right)=5\)
\(\Leftrightarrow\left(x+y-2\right)\left(x+3y\right)=5\)
Bảng giá trị:
| x+y-2 | -5 | -1 | 1 | 5 |
| x+3y | -1 | -5 | 5 | 1 |
| x | -4 | 4 | 2 | 10 |
| y | 1 | -3 | 1 | -3 |
Vậy \(\left(x;y\right)=\left(-4;1\right);\left(4;-3\right);\left(2;1\right);\left(10;-3\right)\)
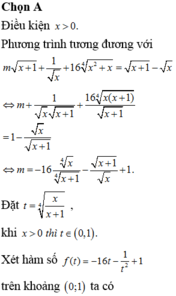
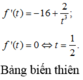
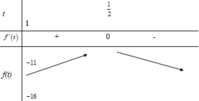
Ta có \(0< 3y^2+1< 4y^2+4\)
=> \(y^4< y^4+3y^4+1< \left(y^2+2\right)^2\)
=> \(y^4< x^4< \left(y^2+2\right)^2\)
Mà x,y nguyên
=> \(x^2=y^2+1\)
=> \(y^4+2y^2+1=y^4+3y^2+1\)
=> \(y=0\)=> x=0
Vậy (x,y)=(0;0)