Nguyên tố X gồm 3 đồng vị. Biết tổng số khối của 3 đồng vị =75 . Biết:
•Số khối của đồng vị thứ 2 bằng trung bình cộng 2 số khối còn lại .
• Đồng vị 1 có số protein bằng số nơtron.
• Đồng vị 3 chiếm 11,4% về số lượng nguyên tử và có số nơtron nhiều hơn đồng vị 2 là 1 hạt .
a) Tìm A1,A2,A3 và n1,n2,n3.
b) Tìm % số lượng của 2 loại đồng vị còn lại



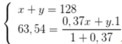
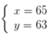

a, Theo đề ta có : A1 + A2 + A3 = 75 (I)
Mặt khác : A2 = \(\frac{A1+A3}{2}\) <=> A1 - 2A2 + A3 = 0 (II)
* Z = N1 <=> 2Z = A1 <=> Z = \(\frac{A1}{2}\) (III)
N3 = N2 + 1
<=> A3 = A2 + 1 <=.> - A2 + A3 = 1 (IV)
Giair hệ (I) , (II) , (III) ,(IV) ta được :
A1 = 24 ; A2 = 25 : A3 = 26
và N1 = Z = A1/2 = 24/2 = 12 (hạt)
N2 = A2 - Z = 25 - 12 = 13 (hạt)
N3 = A3 - Z = 26 - 12 = 14 (hạt)
b, đề thiếu dữ kiện của nguyên tử khối trung bình nha
Với Z = 12 ta kết luận được đây là nguyên tố Mg có nguyên tử khối trung bình ( được ghi trong bảng tuần hoàn ) là : 24,3050
Gọi %A1 = a (%) , %A2 = 100% - a% - 11,4% = (88,6 - a) (%)
Theo đề ta có :
24a + 25* (88,6 - a ) + 11,4*26 = 100* 24,3050
<=> a = 80,9 (%)
Vậy thành phần phần trăm số nguyên tử của đồng vị A1 là 80,9
thành phần phần trăm số nguyên tử của đồng vị A2 là : 88,6% - 80,9% = 7,7 %
c) có 50 nguyên tử của đồng vị thứ 2 tính số nguyên tử của 2 đồng vị còn lại
Bạn giải giúp mình câu đây được không