Tam giác ABC có cạnh BC cố định, đường trung tuyến BM = 1cm. Hỏi đỉnh A di động
trên đường nào?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ML
0
Q
22 tháng 7 2017
[toán 9]bài tập về sự xác định đường tròn | Diễn đàn HOCMAI - Cộng đồng học tập lớn nhất Việt Nam
BV
0
8 tháng 10 2016
Kẻ AK vuông góc BC. Gọi G là trọng tâm tam giác ABC và N là trung điểm BC. Kẻ GI vuông góc với AK
\(\Rightarrow\)GI // BC
\(\Rightarrow\frac{IK}{AK}=\frac{IK}{3}=\frac{GN}{AN}=\frac{1}{3}\)
\(\Rightarrow IK=1\)
Mà IK chính là khoản cách từ G đến BC
Vậy trọng tâm G nằm trên đường thẳng song song với BC và cách BC 1 khoản là 1 cm
17 tháng 8 2020
giả thiết: CN vuông góc với AN , góc A1= góc A2, M là tđ
( Hình vẽ chỉ mang t/c minh họa)
Xét tam giác ANC vuông tại N có M là trung điểm AC=> AM=MN=MC (luông đúng khi A thay đổi)
=> tam giác AMN cân tại M => góc A2 = góc ANM
Mà A1=A2 (AN là phân giác góc BAC)=> A1=ANM(so le trong)=> MN//AB
Xét tam giác ABC có M là trung điểm của AC và MN//AB(cmt)=> MN đi qua trung điểm của BC
Vậy....
1 tháng 5 2017
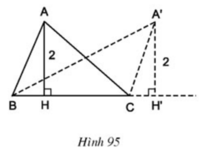
Gọi h (AH) là đường cao của \(\Delta ABC\) thì h là hằng số không đổi và cạnh đáy BC bằng a cố định .
Ta có : \(S_{ABC}=\dfrac{1}{2}BC.AH=\dfrac{1}{2}a.h\) không đổi .
Vậy diện tích tam giác ABC luôn không đồi nếu có đáy BC cố định và đỉnh A di động trên 1 đường thẳng d cố định song song với đường thẳng BC .
CM
28 tháng 4 2017
Đỉnh A của các tam giác đó nằm trên đường thẳng song song với BC và cách BC một khoảng bằng 2 cm