Cho hai đường tròn (O;R)và (O';R') tiếp xúc ngoài tại A .vẽ tiếp tuyến chung MN.M thuộc đường tròn (O) và N thuộc đường tròn (O') tiếp tuyến chung tại A cắt MN tại I
chứng minh
a) Góc MAN=90o;Góc OIO'=90o
b)MN=2\(\sqrt{R.R'}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc ABO+góc ACO=180 độ
=>ABOC nội tiếp
b: Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc BC tại H
=>AH*AO=AB^2
Xét ΔABE và ΔADB có
góc ABE=góc ADB
góc BAE chung
=>ΔABE đồng dạng với ΔADB
=>AB^2=AE*AD=AH*AO

a: Xét ΔABE và ΔADB co
góc ABE=góc ADB
góc BAE chung
=>ΔABE đồng dạng với ΔADB
=>AB/AD=AE/AB
=>AB^2=AD*AE
Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc BC tại H
=>AH*AO=AB^2=AE*AD
=>AH/AD=AE/AO
=>ΔAHE đồng dạng với ΔADO
=>góc AHE=góc ADO
=>góc OHE+góc ODE=180 độ
=>OHED nội tiếp
b: OHED nội tiếp
=>góc HED+góc HOD=180 độ
BD//AO
=>góc BDO+góc HOD=180 độ
=>góc BDO=góc HED
góc BCD+góc BDC=90 độ
góc BCD=góc BED
=>góc HED+góc BED=90 độ
=>HE vuông góc BF tại E


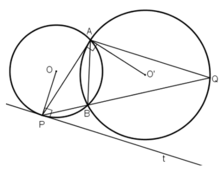
(O; R) và (O’; R’) tiếp xúc ngoài với nhau
⇒ OO’ = R + r.
O’A ⊥ BP, OB ⊥ BP ⇒ O’A // OB
⇒ ΔPAO’  ΔPBO
ΔPBO

⇒ OB = 2.O'A hay R = 2.r
và OP = 2.O’P ⇒ O’P = OO’ = R + r = 3.r
ΔO’AP vuông tại A nên:
O ’ P 2 = O ’ A 2 + A P 2
⇔ ( 3 r ) 2 = r 2 + 4 2 ⇔ 8 r 2 = 16 ⇔ r 2 = 2
Diện tích hình tròn (O’; r) là: S = π . r 2 = 2 π ( c m 2 ) .


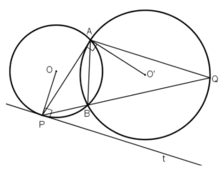
(O; R) và (O’; R’) tiếp xúc ngoài với nhau
⇒ OO’ = R + r.
O’A ⊥ BP, OB ⊥ BP ⇒ O’A // OB
⇒ ΔPAO’  ΔPBO
ΔPBO

⇒ OB = 2.O'A hay R = 2.r
và OP = 2.O’P ⇒ O’P = OO’ = R + r = 3.r
ΔO’AP vuông tại A nên: O ' P 2 = O ' A 2 + A P 2
⇔ ( 3 r ) 2 = r 2 + 4 2 ⇔ 8 r 2 = 16 ⇔ r 2 = 2
Diện tích hình tròn (O’; r) là: S = π · r 2 = 2 π cm 2



Kiến thức áp dụng
Trong một đường tròn:
+ Số đo của góc nội tiếp bằng một nửa số đo của cung bị chắn.
+ Số đo của góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn.


a)
Gọi giao của AM và OI là H, giao của O'I và AN là K
Ta có: IO là phân giác \(\widehat{MIA}\) ( tính chất tiếp tuyến)
IO' là phân giác \(\widehat{NIA}\) ( tính chất tiếp tuyến)
Do đó suy ra \(\widehat{OIO'}\) =90o (2 tia phân giác của hai góc kề bù vuông góc với nhau)
Ta có: \(OA=OM=R\)
\(\Rightarrow\) O thuộc đường trung trực của AM (1)
Ta có: \(IA=IM\) ( tính chất tiếp tuyến)
\(\Rightarrow\) I thuộc đường trung trực của AM (2)
(1)(2)\(\Rightarrow\) OI là trung trực của AM
\(\Rightarrow\)\(\widehat{IHA}\) \(=90^o\)
Chứng minh tương tự: O'I là trung trực của AN
\(\Rightarrow\) \(\widehat{IKA}\) \(=90^o\)
Do đó AHIK là hình chữ nhật
\(\Rightarrow\) \(\widehat{MAN}\)\(=90^o\)
b)
Giả sử R>R'
Từ O'kẻ đường thẳng song song với MN cắt OM tại D
\(\Rightarrow\) \(OD\)//\(MN\)
\(\Rightarrow\)\(\widehat{O'DM} \)\(=90^o\)
Mà \(\widehat{OMN}\)=90o, \(\widehat{O'NM}\) =90o
\(\Rightarrow MNO'D\) là hình chữ nhật
\(\Rightarrow MN=O'D,MD=NO'=R',OD=OM-MD=R-R'\)
Vì \(\widehat{O'DM}\) =90
\(\Rightarrow\) \(\Delta ODO'\) là tam giác vuông
\(\Rightarrow DO^2=OO'^2-OD^2\)( định lý pythagor)
\(\Rightarrow DO^2=\left(R+R'\right)^2-\left(R-R'\right)^2=4RR'\)
\(\Rightarrow DO=2\sqrt{RR'}\)
\(\Rightarrow MN=2\sqrt{R.R'}\left(đpcm\right)\)