Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(A=n^5-n=n\left(n^4-1\right)=n\left(n^2-1\right)\left(n^2+1\right)=n\left(n-1\right)\left(n+1\right)\left(n^2+1\right)\\ \)
- Nếu n chia hết cho 5 thì A chia hết cho 5
- Nếu n chia 5 dư 1 thì (n-1) chia hết cho 5 => A chia hết cho 5
- Nếu n chia 5 dư 2 thì n = 5k +2 => n2 + 1 = 25k2 + 20k + 4 + 1 chia hết cho 5 => A chia hết cho 5
- Nếu n chia 5 dư 3 thì n = 5k +3 => n2 + 1 = 25k2 + 30k + 9 + 1 chia hết cho 5 => A chia hết cho 5
- Nếu n chia 5 dư 4 thì (n+1) chia hết cho 5 => A chia hết cho 5
n thuộc N lớn hơn hoặc bằng 2 chỉ có 5 trường hợp có số dư như trên khi chia cho 5. Nên A chia hết cho 5 với mọi n thuộc N lớn hơn hoặc bằng 2.


Theo Von Neumanm. Cấu trúc chung của máy tính gồm 3 phần:
+ Bộ xử lí trung tâm (CPU)
+ Bộ nhớ
+ Thiết bị vào/ra
* Bộ xử lí trung tâm(CPU) được xem là bộ não của máy tính thực hiện các chức năng tính toán, điều khiển, điều phối mọi hoạt động của máy tính theo sự chỉ dẫn của chương trình.
* Bộ nhớ dùng để lưu chương trình và dữ liệu. Được chia ra làm hai loại: bộ nhớ trong và bộ nhớ ngoaì.

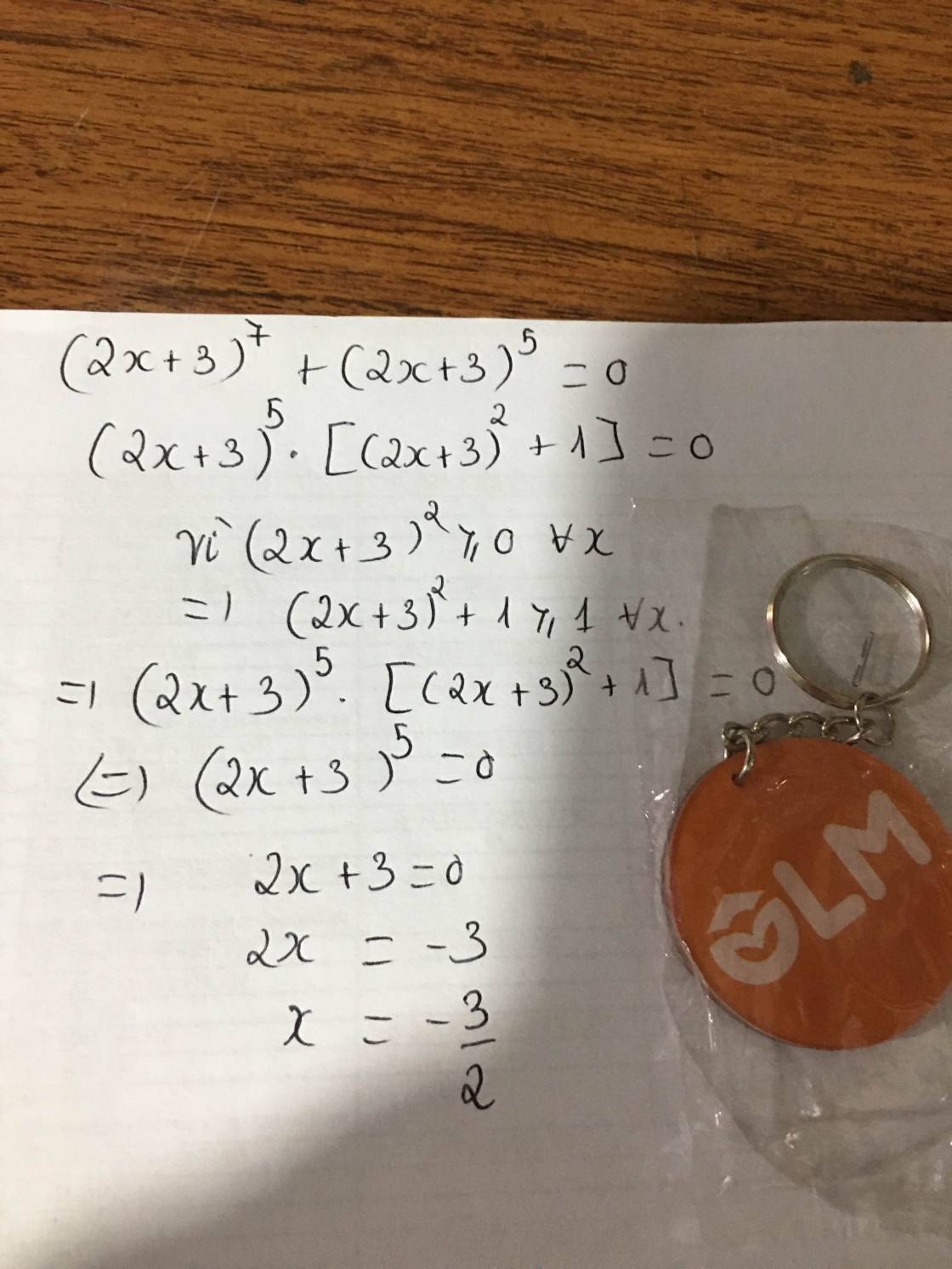


a ) \(\frac{x}{15}=\frac{y}{7}\)và \(x-2y=16\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{15}=\frac{y}{7}=\frac{x}{15}=\frac{2y}{14}=\frac{x-2y}{15-14}=\frac{16}{1}=16\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{15}=16\\\frac{2y}{14}=16\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=240\\y=112\end{cases}}\)
b ) Từ \(\frac{x}{4}=\frac{y}{5}\)\(\Rightarrow\)\(\frac{x}{4}.\frac{1}{6}=\frac{y}{5}.\frac{1}{6}=\frac{x}{24}=\frac{y}{30}\)( 1 )
Từ \(\frac{y}{6}=\frac{z}{7}\)\(\Rightarrow\)\(\frac{y}{6}.\frac{1}{5}=\frac{z}{7}.\frac{1}{5}=\frac{y}{30}=\frac{z}{35}\)( 2 )
Từ ( 1 ) và ( 2 ) ta có :\(\frac{x}{24}=\frac{y}{30}=\frac{z}{35}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{24}=\frac{y}{30}=\frac{z}{35}=\frac{2x}{48}=\frac{y}{30}=\frac{z}{35}=\frac{2x+y-z}{48+30-35}=\frac{15}{43}\)
\(\Rightarrow\hept{\begin{cases}\frac{2x}{48}=\frac{15}{43}\\\frac{y}{30}=\frac{15}{43}\\\frac{z}{35}=\frac{15}{43}\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=\frac{360}{43}\\y=\frac{450}{43}\\z=\frac{525}{43}\end{cases}}\)