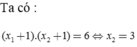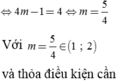4cos24x+cos4x-5=0 có 2 nghiệm thuộc khoảng(0,\(\frac{3\pi}{2}\)) là x1,x2. Khi đó |x1-x2| là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 5 2018
Đáp án B
P T ⇔ 2 2 x 2 − 5 2 x + 2 = 0 ⇔ 2 x = 2 2 x = 1 2 ⇔ x = 1 x = − 1 ⇒ x 1 = − 1 x 2 = 1 ⇒ x 2 − x 1 = 2.
12 tháng 8 2021
3x^2 - 5x - 2 = 0
(a = 3; b = -5; c = -2)
ta có x1, x2 là nghiệm của pt nên : x1 + x2 = -b/a = -(-5)/3 = 5/3
vậy_
VC
Vũ Cao Minh⁀ᶦᵈᵒᶫ ( ✎﹏IDΣΛ亗 )
CTV
VIP
12 tháng 8 2021
Áp dụng hệ thức Vi - ét ta có : x1 + x2 = \(-\frac{b}{a}=-\frac{-5}{3}=\frac{5}{3}\)
Hoặc chưa học ở lớp 8 thì \(3x^2-5x-2=3x^2-6x+x-2=3x\left(x-2\right)+\left(x-2\right)\)
\(=\left(3x+1\right)\left(x-2\right)=0\Leftrightarrow\orbr{\begin{cases}x1=-\frac{1}{3}\\x2=2\end{cases}}\Leftrightarrow x1+x2=-\frac{1}{3}+2=\frac{5}{3}\)
DD
Đoàn Đức Hà
Giáo viên
13 tháng 8 2021
\(3x^2-5x-2=0\)
\(\Leftrightarrow3x^2-6x+x-2=0\)
\(\Leftrightarrow\left(3x-1\right)\left(x-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{1}{3}\\x=2\end{cases}}\)
\(A=x_1+x_2=\frac{1}{3}+2=\frac{7}{3}\).
CM
28 tháng 5 2019
Chọn B.
Phương pháp:
Đưa phương trình về dạng tích, giải phương trình tìm nghiệm và tìm điều kiện để bài toán thỏa.
