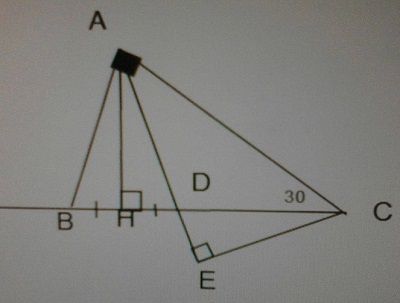
Cho tam giác ABC vuông tại A có C = 30 độ,Đường cao AH.Trên HC lấy điểm D sao cho HD=HB.Từ C kẻ CE vuông góc AD,Ethuộc AD.C/m rằng
a,tam giác ABD là tam giác đều
b,EH // AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 7 2019
a,Xét tam giác ABD có AH là đường cao( AH vuông góc với BC)
đồng thời AH là đường trung tuyến( HD=HB)
=> tam giác ABD cân tại A(1)
lại có tam giác ABC vuông tại A, góc C=30 độ
=> góc B=90 độ-gócc
=90-30 =60 độ(2)
từ(1) (2)=> tam giác ABD đều
21 tháng 1 2017
Bài 1:
a)+ Vì AB = ACNÊN
==>Tam giác ABC cân tại A
==>góc ABI = góc ACI
+ Xét tam giác ABI và tam giác ACI có:
AI là cạch chung
AB = AC(gt)
BI = IC ( I là trung điểm của BC)
Vậy tam giác ABI = tam giác ACI (c.c.c)
==> góc BAI = góc CAI ( 2 góc tương ứng )
==>AI là tia phân giác của góc BAC
b)
Xét tam giác BAM và tam giác BAN có:
AB = AC (gt)
góc B = góc C (cmt)
BM = CN ( gt )
Vậy tam giác BAM = tam giác CAN (c.g.c)
==> AM = AN (2 cạnh tương ứng)
c)
vì tam giác BAI = tam giác CAI (cmt)
==>góc AIB = góc AIC (2 góc tương ứng)
Mà góc AIB+ góc AIC = 180độ ( kề bù)
nên AIB=AIC=180:2=90
==>AI vuông góc với BC
a)Ta có :\(\widehat{BAC}+\widehat{ACB}+\widehat{ABC}=180\)
THay số \(\Rightarrow\widehat{ABC}=60\) (1)
Xét \(\Delta BAH\perp\) tại H và \(\Delta DAH\perp\) tại H có:
BH=HD(gt)
AH chung
\(\Rightarrow\Delta BAH=\Delta DAH\left(2cgv\right)\)
\(\Rightarrow AB=AD\) và \(\widehat{ABH}=\widehat{ADH}\) (2)
Từ (1) vá (2) \(\Rightarrow\Delta ABD\) đều (đpcm)
b) mk làm tắt nhé!
Xét \(\Delta HDA\perp\) tại H và \(\Delta EDC\perp\) tại E có:
..............
\(\Rightarrow\Delta HDA=\Delta EDC\left(ch-gn\right)\)
=> HD=DE
\(\Rightarrow\Delta HDE\) cân tại D\(\Rightarrow\widehat{DHE}=\widehat{DEH}\)
Ta có:\(\widehat{ADH}+\widehat{HDE}=180\Leftrightarrow\widehat{HDE}=120\)
\(\widehat{HDE}+\widehat{DHE}+\widehat{DEH}=180\Rightarrow\widehat{DEH}=\widehat{DHE}=30\)
Vì \(\widehat{DCA}=\widehat{DHE}=30\)
mà 2 góc này ở vị trí so le trong =>HE//AC(đpcm)
a) Ta có : tam giác ABC vuông tại A có góc C = 300 => \(\widehat{B}\)= 600(1)
Xét \(\Delta ABD\)có : BH = DH (gt), AH \(\perp\)BD => \(\Delta ABD\)cân tại A (2)
Từ (1), (2) => tam giác ABD đều (đpcm)
b) Theo câu a) \(\Delta ABD\)đều => \(\widehat{BAD}\)= 600 => \(\widehat{CAD}\)= 300.
Mà \(\widehat{ACB}\)= 300 (gt) => \(\Delta ACD\)cân tại D => AD = CD
Xét \(\Delta AHD\)và \(\Delta CED\)có :
AD = CD (cmt)
\(\widehat{D_1}=\widehat{D_2}\)(đối đỉnh)
=> \(\Delta AHD\)= \(\Delta CED\)(cạnh huyền - góc nhọn)
=> HD = DE => \(\Delta HDE\)cân tại D
Xét \(\Delta HDE\&\Delta ACD\)là 2 tam giác cân có \(\widehat{HDE}=\widehat{ADC}\)(2 góc ở đỉnh bằng nhau) nên các góc ở đáy cũng bằng nhau.
Hay \(\widehat{HED}=\widehat{DAC}\)(2 góc bằng nhau ở vị trí so le trong)
=> HE // AC (đpcm)